题目内容
9. 已知抛物线y=ax2+bx经过点A(-3、-3)和点P(t、0),且t≠0
已知抛物线y=ax2+bx经过点A(-3、-3)和点P(t、0),且t≠0 (1)若抛物线的对称轴经过点A,如图所示,则此时y的最小值为-3;并写出此时t的值为-6;
(2)若t=-4,求a、b的值.
(3)直接写出使抛物线开口向下的一个t的值.
分析 (1)直接利用二次函数图象得出其最值以及t的值;
(2)利用待定系数法求出a,b的值;
(3)利用函数图象结合抛物线y=ax2+bx经过点A(-3、-3),即可得出t的取值范围.
解答 解:(1)如图所示:若抛物线的对称轴经过点A,则此时y的最小值为:-3;此时t的值为:-6;
故答案为:-3,-6;
(2)若t=-4,则二次函数图象经过A(-3,-3),P(-4,0),
则$\left\{\begin{array}{l}{-3=9a-3b}\\{0=16a-4b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=4}\end{array}\right.$;
(3)使抛物线开口向下的一个t的值可以为:1(t>-3即可).
点评 此题主要考查了二次函数的性质以及待定系数法求出二次函数解析式,正确利用数形结合分析是解题关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
20.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工王师傅2013年月退休金为1800元,2015年达到2460元.设王师傅的月退休金从2013年到2015年年平均增长率为x,可列方程为( )
| A. | 2460(1-x)2=1800 | B. | 1800(1+x)2=2460 | ||
| C. | 1800(1-x)2=2460 | D. | 1800+1800(1+x)+1800(1+x)2=2460 |
17. 有理数a,b在数轴上的对应点的位置如图所示,则( )
有理数a,b在数轴上的对应点的位置如图所示,则( )
 有理数a,b在数轴上的对应点的位置如图所示,则( )
有理数a,b在数轴上的对应点的位置如图所示,则( )| A. | a+b=0 | B. | a+b>0 | C. | |a|>|b| | D. | a-b>0 |
4.若分式$\frac{{x}^{2}-x-6}{{x}^{2}+3x+2}$的值为0,则x的值为( )
| A. | 3或-2 | B. | 3 | C. | -2 | D. | -3或2 |
14.下面各题的计算正确的是( )
| A. | a2•a4=a8 | B. | a8÷a3=a5 | C. | (a2)3=a5 | D. | 2a2•3ab2=6a2b2 |
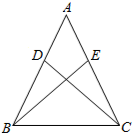 已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.
已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.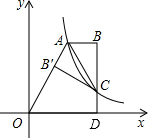 如图,双曲线$y=\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则
如图,双曲线$y=\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则 如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.
如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.