题目内容
下列各多项式中，能用平方差公式分解因式的是（ ）
| A、-x2+9 |
| B、-x2-9 |
| C、x2+9 |
| D、x2+2y2 |
考点：因式分解-运用公式法
专题：
分析：能用平方差公式法进行因式分解的式子的特点：两项平方项；符号相反．
解答：解：A、-x2+9能用平方差公式分解因式，正确；
B、-x2-9的两项符号相同，不能分解，故错误；
C、x2+9的两项符号相同，不能分解，故错误；
D、x2+2y2的2不是平方项，也不能用平方差公式分解因式，故错误．
故选：A．
B、-x2-9的两项符号相同，不能分解，故错误；
C、x2+9的两项符号相同，不能分解，故错误；
D、x2+2y2的2不是平方项，也不能用平方差公式分解因式，故错误．
故选：A．
点评：本题考查用平方差公式进行因式分解的式子的特点，需熟记．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
2014年6月10日中商情报网报道，6月9日余额宝的万份收益为1.2719元，下列四舍五入法按要求对1.2719分别取近似值，其中不正确的是（ ）
| A、精确到个位是1 |
| B、精确到十分位是1.3 |
| C、精确到0.01是1.27 |
| D、精确到千分位是1.271 |
下列说法错误的是（ ）
| A、全等三角形的对应边相等 |
| B、全等三角形的对应角相等 |
| C、若两个三角形全等且有公共顶点，则公共顶点就是对应顶点 |
| D、若两个三角形全等，则对应边所对的角是对应角 |
如图，由△DEF平移得到△ABC，则平移的方向是
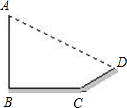在同一时刻的物高与水平地面上的影长成正比例．小莉发现垂直地面的电线杆AB的影子落在地面和土坡上，影长分别为BC和CD，经测量得BC=20m，CD=8m，CD与地面成30°角，且此时测得垂直于地面的1m长标杆在地面上影长为2m，则电线杆AB的长度为下列运算中正确的是（ ）
| A、（3a）2=6a2 |
| B、2a2•a3=2a5 |
| C、（ab）4=ab4 |
| D、a2+a2=a4 |
如图是用一张长方形纸条折成的，如果∠1=130°，那么∠2=在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（ ）
A、
| ||
B、
| ||
| C、9 | ||
| D、6 |