题目内容
在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（ ）
A、
| ||
B、
| ||
| C、9 | ||
| D、6 |
考点：勾股定理
专题：
分析：设点C到斜边AB的距离是h，根据勾股定理求出AB的长，再根据三角形的面积公式即可得出结论．
解答：解：设点C到斜边AB的距离是h，
∵在Rt△ABC中，∠C=90°，AC=9，BC=12，
∴AB=
=15，
∴h=
=
．
故选A．
∵在Rt△ABC中，∠C=90°，AC=9，BC=12，
∴AB=
| 122+92 |
∴h=
| 12×9 |
| 15 |
| 36 |
| 5 |
故选A．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
下列各多项式中，能用平方差公式分解因式的是（ ）
| A、-x2+9 |
| B、-x2-9 |
| C、x2+9 |
| D、x2+2y2 |
下列计算正确的是（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
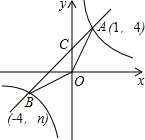如图，已知：反比例函数y=