题目内容
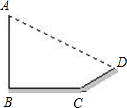 在同一时刻的物高与水平地面上的影长成正比例.小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,则电线杆AB的长度为
在同一时刻的物高与水平地面上的影长成正比例.小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,则电线杆AB的长度为考点:相似三角形的应用,解直角三角形的应用-坡度坡角问题
专题:
分析:构造相应的直角三角形,利用勾股定理及影长与实物比求解.
解答: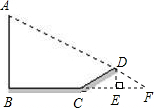 解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.
解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.
∵∠DCE=30°,CD=8米,
∴CE=CD•cos∠DCE=8×
=4
(米),
∴DE=4米,
设AB=x,EF=y,
∵DE⊥BF,AB⊥BF,
∴△DEF∽△ABF,
∴
=
,即
=
…①,
∵1米杆的影长为2米,根据同一时间物高与影长成正比可得,
=
…②,
①②联立,解得x=14+2
(米).
故答案为:(14+2
)m.
 解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.
解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.∵∠DCE=30°,CD=8米,
∴CE=CD•cos∠DCE=8×
| ||
| 2 |
| 3 |
∴DE=4米,
设AB=x,EF=y,
∵DE⊥BF,AB⊥BF,
∴△DEF∽△ABF,
∴
| DE |
| AB |
| EF |
| BF |
| 4 |
| x |
| x | ||
20+4
|
∵1米杆的影长为2米,根据同一时间物高与影长成正比可得,
| 1 |
| 2 |
| x | ||
20+4
|
①②联立,解得x=14+2
| 3 |
故答案为:(14+2
| 3 |
点评:考查相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.作出两条辅助线构造出2个直角三角形是解决本题的突破点.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
下列各多项式中,能用平方差公式分解因式的是( )
| A、-x2+9 |
| B、-x2-9 |
| C、x2+9 |
| D、x2+2y2 |
 如图所示,将△ABC平移得到△A′B′C′,则图中与线段AA′平行且相等的线段为
如图所示,将△ABC平移得到△A′B′C′,则图中与线段AA′平行且相等的线段为