题目内容
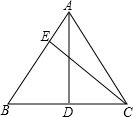如图，在△ABC中，AB=AC=6，BD=CD=4，CE⊥AB于点E，求线段BE的长．考点：勾股定理,三角形的面积,等腰三角形的性质
专题：
分析：由AB=AC，D为BC中点，利用三线合一得到AD垂直于BC，在直角三角形ABD中，利用勾股定理求出AD的长，再利用三角形面积法求出CE的长，在直角三角形BEC中，利用勾股定理求出BE的长即可．
解答：解：∵在△ABC中，AB=AC=6，BD=CD=4，
∴AD⊥BC，
在Rt△ABD中，根据勾股定理得：AD=
=2
，
∵S△ABC=
BC•AD=
AB•CE，
∴CE=
=
，
在Rt△BEC中，根据勾股定理得：BE=
=
．
∴AD⊥BC，
在Rt△ABD中，根据勾股定理得：AD=
| 62-42 |
| 5 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
8×2
| ||
| 6 |
8
| ||
| 3 |
在Rt△BEC中，根据勾股定理得：BE=
| BC2-EC2 |
| 16 |
| 3 |
点评：此题考查了勾股定理，三角形的面积，以及等腰三角形的性质，熟练掌握勾股定理是解本题的关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
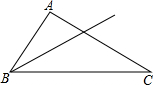如图，在△ABC中，∠A=105°，直线BD交AC于D，把三角形沿着直线BD翻折，点A恰好落在边CB上，如果△CBD是等腰三角形，那么∠C等于（ ）| A、15° | B、25° |
| C、30° | D、40° |