题目内容
已知在Rt△ABC中,∠C=90°,AC=5,BC=12,斜边AB的中点为点D.
(1)若以点D为圆心,6.5为半径画圆,试判断A,B,C三点与圆O的位置关系;
(2)若以点A为圆心画圆⊙A,要想使B,C,D三点中至少有一点在圆内,至少有一点在圆外,则⊙A的半径的取值范围是多少?
(1)若以点D为圆心,6.5为半径画圆,试判断A,B,C三点与圆O的位置关系;
(2)若以点A为圆心画圆⊙A,要想使B,C,D三点中至少有一点在圆内,至少有一点在圆外,则⊙A的半径的取值范围是多少?
考点:点与圆的位置关系
专题:
分析:(1)根据题意可求得Rt△ABC的斜边BC的长,进而求得AD、BD、DC的长,与半径相比即可得到A,B,C三点与圆O的位置关系.
(2)根据AC、AD、AB的长即可判定⊙A的半径的取值范围.
(2)根据AC、AD、AB的长即可判定⊙A的半径的取值范围.
解答: 解:(1)如图1,∵∠C=90°,
解:(1)如图1,∵∠C=90°,
∴AB=
=
=13
∵D是斜边AB的中点,
∴CD=AD=BD=
AB=6.5,
∴A,B,C三点在圆D上;
(2)∵AC=5,AD=6.5,AB=13,
∴要想使B,C,D三点中至少有一点在圆内,至少有一点在圆外,则⊙A的半径的取值范围是5<r<13;
 解:(1)如图1,∵∠C=90°,
解:(1)如图1,∵∠C=90°,∴AB=
| AC2+BC2 |
| 52+122 |
∵D是斜边AB的中点,
∴CD=AD=BD=
| 1 |
| 2 |
∴A,B,C三点在圆D上;
(2)∵AC=5,AD=6.5,AB=13,
∴要想使B,C,D三点中至少有一点在圆内,至少有一点在圆外,则⊙A的半径的取值范围是5<r<13;
点评:此题主要考查了点与圆的位置关系,解决此类问题可通过比较圆心到点距离与圆半径大小关系完成判定.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
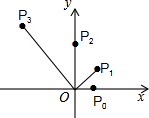 如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )
如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )A、(22014•
| ||||
B、(22012•
| ||||
C、(-22013•
| ||||
| D、(0,-22014) |
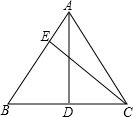 如图,在△ABC中,AB=AC=6,BD=CD=4,CE⊥AB于点E,求线段BE的长.
如图,在△ABC中,AB=AC=6,BD=CD=4,CE⊥AB于点E,求线段BE的长. 在等边△ABC中,D是AC中点,E为BC延长线一点,且DB=DE,求证:△DCE是等腰三角形.
在等边△ABC中,D是AC中点,E为BC延长线一点,且DB=DE,求证:△DCE是等腰三角形.