题目内容
10.已知a,b,x,y都为实数,且y+|$\sqrt{x}$-2|=1-a2,|x-4|=3y-3-b2,则a+b+x+y的值为5.分析 由3(y-1)=|x-4|+b2≥0得y≥1,由1-y=|$\sqrt{x}$-2|+a2≥0得y≤1,即可知y=1,再根据非负数的性质可分别得x、a、b的值,代入即可得答案.
解答 解:∵3(y-1)=|x-4|+b2≥0,
∴y≥1,
∵1-y=|$\sqrt{x}$-2|+a2≥0,
∴y≤1,
则y=1,
∴x-4=0,即x=4,b=0,a=0,
则a+b+x+y=0+0+4+1=5,
故答案为:5.
点评 本题主要考查非负数的性质,熟练掌握非负数的几种形式及其性质是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.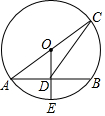 如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
 如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )| A. | AB=2DE | B. | AB=3DE | C. | AB=4DE | D. | 2AB=3DE |
15.下列四个数中,在$-\sqrt{2}$到0之间的数是( )
| A. | -2 | B. | -1 | C. | $-\frac{3}{2}$ | D. | 1 |
20.以下面每组中的三条线段为边的三角形中,是直角三角形的是( )
| A. | 1 3 4 | B. | 1.5 2 2.5 | C. | 4 5 6 | D. | 7 8 9 |