题目内容
15.已知a,b,c,d都是正数,且满足a-2=2,b-3=3,c-4=4,d-5=5,请你探究a,b,c,d中哪一个数最小?分析 先求出a、c的值,再比较出a3与b3的大小,再求出b,d的值,比较出b15与d15的大小即可.
解答 解:∵a-2=2,b-3=3,c-4=4,d-5=5,
∴$\frac{1}{{a}^{2}}$=2,$\frac{1}{{b}^{3}}$=3,$\frac{1}{{c}^{4}}$=4,$\frac{1}{{d}^{5}}$=5,
∵a,b,c,d都是正数,
∴a=c=$\frac{\sqrt{2}}{2}$,b3=$\frac{1}{3}$,d5=$\frac{1}{5}$,
∴a3=$\frac{2\sqrt{2}}{8}$=$\frac{\sqrt{2}}{4}$≈$\frac{1.41}{4}$≈0.35>$\frac{1}{3}$,
∴a=c>b.
∵b=$\root{3}{\frac{1}{3}}$,d=$\root{5}{\frac{1}{5}}$
∴b15=($\frac{1}{3}$)5=$\frac{1}{243}$,d15=($\frac{1}{5}$)3=$\frac{1}{125}$,
∴b15<d15,
∴b<d,
∴b最小.
点评 本题考查的是负整数指数幂,解答此题的关键是把未知数的指数化为相同的数,再比较大小.

练习册系列答案
相关题目
20.下列方程变形中正确的是( )
| A. | 2x+6=-3变形为2x=-3+6 | B. | $\frac{x+3}{3}$-$\frac{x+1}{2}$=1变形为2x+6=-3x+3=6 | ||
| C. | $\frac{2}{5}$x-$\frac{2}{3}$x=$\frac{1}{3}$变形为6x-10x=5 | D. | $\frac{3}{5}$x=2(x-1)+1变形为3x=10(x-1)+1 |
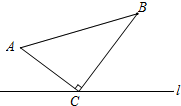 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.