题目内容
4.化简:$\frac{1-x-{x}^{2}+{x}^{3}}{1-2|x|+{x}^{2}}$.分析 原式变形后,分x大于等于0与x小于0两种情况化简得到结果即可.
解答 解:原式=$\frac{(1-x)-{x}^{2}(1-x)}{(1-|x|)^{2}}$=$\frac{(1+x)(1-x)^{2}}{(1-|x|)^{2}}$,
当x≥0时,原式=$\frac{(1+x)(1-x)^{2}}{(1-x)^{2}}$=1+x;
当x<0时,原式=$\frac{(1+x)(1-x)^{2}}{(1+x)^{2}}$=$\frac{(1-x)^{2}}{1+x}$.
点评 此题考查了约分,找出分式分子分母的公因式是约分的关键.

练习册系列答案
相关题目
19.下列四个方程的解正确的是( )
| A. | $\frac{4}{3}x=\frac{4}{3}$,x=1 | B. | 4x-5=0,x=$\frac{4}{5}$ | C. | 4x-0.12=0,x=0.3 | D. | $\frac{3}{5}y$-1=7,y=10 |
13.已知函数y=kx+b,其x与y的部分对应值如下表,解关于x的不等式kx+b<0.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 0 | -2 |
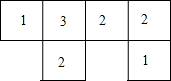 如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.
如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.