题目内容
3.若k为整数,且($\sqrt{2}$+k)($\sqrt{2}$-1)为有理数,则k=1,此时($\sqrt{2}$+k)($\sqrt{2}$-1)=1.分析 已知式子利用多项式乘以多项式法则计算,合并后根据结果为有理数求出整数k的值,求出结果即可.
解答 解:($\sqrt{2}$+k)($\sqrt{2}$-1)=2-$\sqrt{2}$+k$\sqrt{2}$-k=2-k+(k-1)$\sqrt{2}$,
∵k为整数,结果为有理数,
∴k-1=0,
解得:k=1,
则原式=($\sqrt{2}$+1)($\sqrt{2}$-1)=2-1=1,
故答案为:1;1
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.已知函数y=kx+b,其x与y的部分对应值如下表,解关于x的不等式kx+b<0.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 0 | -2 |
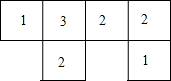 如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.
如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.