题目内容
14．已知x1、x2是方程2x2+5x-4=0的两个实数根，求$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值．分析 首先由根与系数的关系得出两个根的和与积，再把所求式子通分，然后运用完全平方公式，代入两个根的和与积计算即可．
解答 解：∵x1，x2是方程2x2+5x-4=0的两个实数根，
∴x1+x2=-$\frac{5}{2}$，x1•x2=-2，
∴$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{（{x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\frac{25}{4}+4}{-2}$=-$\frac{41}{8}$．
点评 此题主要考查了一元二次方程根与系数的关系，根据题意得出x1+x2=-$\frac{b}{a}$和x1•x2=$\frac{c}{a}$的值是解决问题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
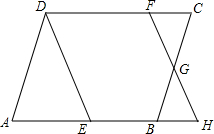如图，E是平行四边形的AB边上一点，连接DE，作FH∥DE，分别交CD、BC、AB的延长线于点F、G、H．求证：△ADE∽△CGH．
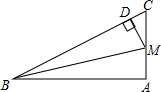△ABC中，∠A=90°，M为AC的中点，MD⊥BC，D为垂足，说明：BD2-CD2=AB2．
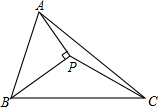如图，在△ABC中，AP垂直∠B的平分线BP于P．若△PBC的面积为12cm2，且△APB的面积是△APC的面积的2倍．则△APB的面积=8cm2．
6．一次函数y=kx+b的图象经过点A（2，3），每当x增加1个单位时，y增加3个单位，则此函数表达式是（ ）
| A． | y=x+3 | B． | y=2x-3 | C． | y=3x-3 | D． | y=4x-4 |
如图所示：AD平分∠BAC交BC于D，写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论．