题目内容
先化简,再求值:(
-
)•
,其中a满足a2+2a-1=0.
| a-2 |
| a2+2a |
| a-1 |
| a2+4a+4 |
| a+2 |
| a-4 |
考点:分式的化简求值
专题:计算题
分析:原式利用乘法分配律计算,通分并利用同分母分式的减法法则计算得到最简结果,把已知方程变形后代入计算即可求出值.
解答:解:原式=[
-
]•
=
-
=
=
=
,
把a2+2a=1代入得:原式=1.
| a-2 |
| a(a+2) |
| a-1 |
| (a+2)2 |
| a+2 |
| a-4 |
=
| a-2 |
| a(a-4) |
| a-1 |
| (a+2)(a-4) |
=
| (a+2)(a-2)-a(a-1) |
| a(a+2)(a-4) |
=
| a-4 |
| a(a+2)(a-4) |
=
| 1 |
| a2+2a |
把a2+2a=1代入得:原式=1.
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设⊙O的半径是6cm,点O到直线l的距离为d,⊙O与直线l有公共点,则( )
| A、d>6cm |
| B、d=6cm |
| C、0≤d<6cm |
| D、0≤d≤6cm |
 如图所示,不能判定AD∥BC的条件是( )
如图所示,不能判定AD∥BC的条件是( )| A、∠2=∠3 |
| B、∠1=∠4 |
| C、∠DAB+∠ABC=180° |
| D、∠ADC+∠BCD=180° |
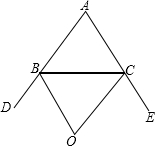 如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.
如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由. 如图,已知AD∥BC,AD⊥CD,AC⊥AB,已知AD=4,BC=9,则AC=
如图,已知AD∥BC,AD⊥CD,AC⊥AB,已知AD=4,BC=9,则AC=
 如图,在△ABC中,AC=BC=3,AB=3
如图,在△ABC中,AC=BC=3,AB=3