题目内容
5.先化简,再求值:$\frac{1}{x}÷(\frac{{{x^2}+1}}{{{x^2}-x}}-\frac{2}{x-1})+\frac{1}{x+1}$,其中x=$\frac{1}{3}$.分析 先把分式化简,再代入求值,即可解答.
解答 解:原式=$\frac{1}{x}$÷$\frac{{x}^{2}+1-2x}{x(x-1)}$+$\frac{1}{x+1}$
=$\frac{1}{x}•\frac{x(x-1)}{(x-1)^{2}}+\frac{1}{x+1}$
=$\frac{1}{x-1}+\frac{1}{x+1}$
=$\frac{2x}{{x}^{2}-1}$
当x=$\frac{1}{3}$时,原式=-$\frac{3}{4}$.
点评 本题考查分式的化简求值,解决本题的关键是先把分式化简,再代入求值.

练习册系列答案
相关题目
16.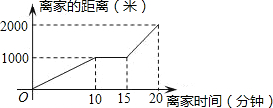 某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
 某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )| A. | 学校离家的距离为1000米 | |
| B. | 修车时间为5分钟 | |
| C. | 到达学校时共用时间20分钟 | |
| D. | 修车后小明骑车的速度是修车前速度的2倍 |
20. 一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.
一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.
 一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.
一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次长跑的全程为( )米.| A. | 2000米 | B. | 2100米 | C. | 2200米 | D. | 2400米 |
14.如果一组数据:6,-2,0,6,4,x的平均数是2,那么x等于( )
| A. | 3 | B. | 4 | C. | -2 | D. | 6 |
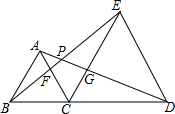 如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.
如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.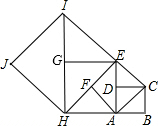 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.