题目内容

20．一次长跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚在此后所跑的路程y（米）与时间t（秒）之间的函数关系如图，则这次长跑的全程为（　　）米．
A．2000米B．2100米C．2200米D．2400米

分析 设小明的速度为a米/秒，小刚的速度为b米/秒，由行程问题的数量关系建立方程组求出其解即可．

解答 解：设小明的速度为a米/秒，小刚的速度为b米/秒，由题意，得
$\left\{\begin{array}{l}{1600+100a=1400+100b}\\{1600+300a=1400+200b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$．
故这次越野跑的全程为：1600+300×2=2200米．
故选C．

点评 本题考查了行程问题的数量关系的运用，二元一次方程组的解法的运用，解答时由函数图象的数量关系建立方程组是关键．

练习册系列答案
相关题目
10．点P（x，y）先向左平移3个单位，再向上平移4个单位得到P′，则点P′的坐标为（　　）
A．（x-3，y+4）B．（x+3，y-4）C．（x-4，y+3）D．（x+4，y-3）
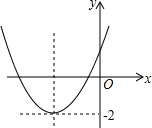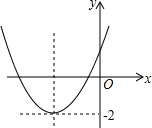11．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：
①abc＜0；②m＜-2；③b2-4ac＜0；④b2-4ac-8a=0
其中正确结论的序号是（　　）
A．①④B．②③C．①②D．②④
8．某品牌专卖店某天销售了13双运动鞋，其尺码统计如表：
尺码（单位：码）3839404142
数量（单位：双）25312
则这13双运动鞋尺码的众数和中位数分别是（　　）
A．40码、39码B．39码、40码C．40码、40码D．39码、39码
15．一次函数y=3x+6的图象经过（　　）
A．第1、2、3象限B．第2、3、4象限C．第1、2、4象限D．第1、3、4象限
5．先化简，再求值：$\frac{1}{x}÷（\frac{{{x^2}+1}}{{{x^2}-x}}-\frac{2}{x-1}）+\frac{1}{x+1}$，其中x=$\frac{1}{3}$．
12．计算2x3•（-x2）的结果是（　　）
A．-2x5B．2x5C．-2x6D．2x6
9．圆锥底面半径是R，母线长是3R，M是底面圆周上一点，从点M拉一根绳子绕圆锥一圈，再回到M点，求这根绳子的最短长度．
10．为促进学校之间的友谊，某县教育局组织了中学生友谊篮球赛，要求每两队之间都进行两次比赛，共要比赛90场，问共有多少个学校组队参加比赛？若设共有x个学校组队参加比赛，可列方程为（　　）
A．$\frac{1}{2}x（x-1）=90$B．$\frac{1}{2}x（x+1）=90$C．x（x-1）=90D．x（x+1）=90

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网