题目内容
20. 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2,过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2,过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.(1)已知OB=CD,求a的值;
(2)已知OB=2CD,求a的值;
(3)你还能提出什么问题?
分析 (1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=-$\frac{1}{2}$x+b即可求得b的值,则A和B的坐标即可求得,△OPD是等腰直角三角形,设OP=a,则D的坐标是(a,a),把x=a代入y=-$\frac{1}{2}$x+b即可求得C的坐标,根据OB=CD即可列方程求得a的值;
(2)同(1)的方法,以及OB=2CD列方程求解;
(3)可以把OB=2CD改成OB=3CD或直接改成OB=nCD即可.
解答 解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=-x+b得-1+b=2,解得b=3,
∴一次函数的解析式为y=-x+3,
把y=0代入y=-x+3得-x+3=0,解得x=6,
∴A点坐标为(6,0);
把x=0代入y=-x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,-a+3),D点坐标为(a,a)
∴a-(-a+3)=3,
∴a=4;
(2)C的坐标是(a,-$\frac{1}{2}$a+3),D点坐标为(a,a),
则CD=a-(-$\frac{1}{2}$a+3)=$\frac{3}{2}$a-3.
∵OB=2CD,
∴3=2($\frac{3}{2}$a-3),
∴a=3;
(3)问题:当OB=nCD时,求a的值.
点评 本题考查了待定系数法求函数的解析式以及等腰直角三角形的性质,把OB与CD的大小关系转化为方程问题是本题的关键.

练习册系列答案
相关题目
19.阅读下面材料,在数学课上,老师提出如下问题:
小颢这样操作的:
老师说:“小颢的做法是正确的.”
请回答:小颢的作图依据是对角线互相垂直平分的四边形是菱形.
| 已知:线段AB. 尺规作图:以线段AB为对角线作一个菱形ADBC. |
| 如图:(1)分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于C、D; (2)作四边形ADBC. 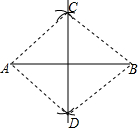 |
请回答:小颢的作图依据是对角线互相垂直平分的四边形是菱形.
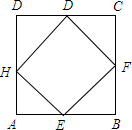 如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.
如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.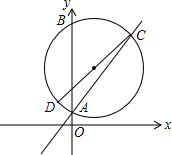 如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.
如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值. 如图,
如图, 如图,点P为双曲线y=$\frac{12}{x}$(x>0)上一点,点A为x轴正半轴上一点,且OP=OA=5,求S△OAP.
如图,点P为双曲线y=$\frac{12}{x}$(x>0)上一点,点A为x轴正半轴上一点,且OP=OA=5,求S△OAP.