题目内容
14.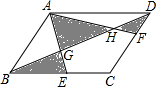 如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?
如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?
分析 设△DFH的面积为S,连接AC.由DF∥AB,CF=2DF,推出$\frac{DF}{AB}$=$\frac{DH}{BH}$=$\frac{FH}{AH}$=$\frac{1}{3}$,可得S△ADH=3s,S△ADF=4s,S△ADC=12S,由AD∥BE,BE=EC,推出$\frac{BE}{AD}$=$\frac{EG}{AG}$=$\frac{BG}{DG}$=$\frac{1}{2}$,可得S△ABE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$S△ADC=6S,求出阴影部分和空白部分的面积即可解决问题.
解答 解:设△DFH的面积为S,连接AC.
∵DF∥AB,CF=2DF,
∴$\frac{DF}{AB}$=$\frac{DH}{BH}$=$\frac{FH}{AH}$=$\frac{1}{3}$,
∴S△ADH=3s,S△ADF=4s,S△ADC=12S,
∵AD∥BE,BE=EC,
∴$\frac{BE}{AD}$=$\frac{EG}{AG}$=$\frac{BG}{DG}$=$\frac{1}{2}$,
∴S△ABE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$S△ADC=6S,
∴S△BEG=2S,S△ABG=4s,
∴S△AGH=S△ABD-S△ABG-S△DFH=12S-4S-S=7S,
∴S阴=2S+7S+S=10S,S空白=24S-10S=14S,
∴S阴:S空白=10S:14S=5:7.
点评 本题考查平行四边形的性质、平行线分线段成比例定理、等高模型等知识,解题的关键是学会利用参数解决问题,属于中考压轴题.

练习册系列答案
相关题目
6.某工厂接到加工600件衣服的订单,预计每天做25件,正好按时完成,后因客户要求提前3天交货,工人则需要提高每天的工作效率,设工人每天应多做x件,依题意列方程正确的是( )
| A. | $\frac{600}{25+x}$-$\frac{600}{25}$=3 | B. | $\frac{600}{25}$+3=$\frac{600}{x}$ | C. | $\frac{600}{25}$-$\frac{600}{x}$=3 | D. | $\frac{600}{25}$-$\frac{600}{25+x}$=3 |
3.线段EF是由线段PQ平移得到的,点P(-2,4)的对应点为E(3,0),则点Q(-3,-1)的对应点F的坐标为( )
| A. | (-8,3) | B. | (-8,-5) | C. | (2,-5) | D. | (2,3) |
4.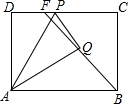 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )| A. | 3 | B. | 2 | C. | 4-$\sqrt{7}$ | D. | 4-$\sqrt{5}$ |
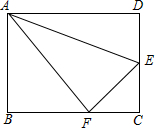 如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°
如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°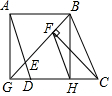 如图,四边形ABHG是正方形,D,C在射线GH上,四边形ABCD是平行四边形,CF⊥BG于F,BG,AD交于点E,连HF.
如图,四边形ABHG是正方形,D,C在射线GH上,四边形ABCD是平行四边形,CF⊥BG于F,BG,AD交于点E,连HF.