题目内容
10．三角形三边之比为1：2：$\sqrt{3}$，则三角形中最大角为（ ）| A． | 60° | B． | 90° | C． | 120° | D． | 135° |
分析 设三角形三边分别为x、2x、$\sqrt{3}$x，根据勾股定理的逆定理进行解答即可．
解答 解：设三角形三边分别为x、2x、$\sqrt{3}$x，
∵x2+（$\sqrt{3}$x）2=4x2，
（2x）2=4x2，
∴x2+（$\sqrt{3}$x）2=（2x）2，
∴这个三角形是直角三角形，
∴三角形中最大角为90°，
故选：B．
点评 本题考查的是勾股定理，掌握勾股定理的逆定理是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，等腰三角形ABC中，BD=CD，AE=DE，求证：CF=2AF．
19．
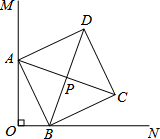如图，∠MON=90°，点B在射线ON上且OB=2，点A在射线OM上，以AB为边在∠MON内部作正方形ABCD，其对角线AC、BD交于点P．在点A从O点出发，沿射线OM的运动过程中，下列说法正确的是（ ）
如图，∠MON=90°，点B在射线ON上且OB=2，点A在射线OM上，以AB为边在∠MON内部作正方形ABCD，其对角线AC、BD交于点P．在点A从O点出发，沿射线OM的运动过程中，下列说法正确的是（ ）| A． | 点P始终在∠MON的平分线上，且线段OP的长有最小值等于$\sqrt{2}$ | |
| B． | 点P始终在∠MON的平分线上，且线段OP的长有最大值等于$\sqrt{2}$ | |
| C． | 点P不一定在∠MON的平分线上，但线段OP的长有最小值等于$\sqrt{2}$ | |
| D． | 点P运动路径无法确定 |
20．二次函数y=2x2-6x+8的顶点坐标为（ ）
| A． | $（{-\frac{3}{2}，\frac{23}{4}}）$ | B． | $（{\frac{3}{2}，\frac{23}{4}}）$ | C． | $（{\frac{3}{2}，\frac{7}{2}}）$ | D． | $（{-\frac{3}{2}，\frac{7}{2}}）$ |