题目内容
2.已知△ABC的高AD的延长线交外接圆于E,H为△ABC的垂心,且HD=$\sqrt{2}$,则DE=$\sqrt{2}$.分析 连结CE,根据直角三角形的性质得到∠1=∠3,根据圆周角定理得到∠2=∠3,得到∠1=∠2,根据等腰三角形三线合一得到答案.
解答 解:连结CE,
∵AD和CF为△ABC的高,
∴∠1+∠B=90°,∠3+∠B=90°,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
∵CD⊥HE,
∴△CEH为等腰三角形,
∴DE=HD=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查的是三角形外接圆和外心的知识,掌握圆周角定理、直角三角形的性质、等腰三角形的三线合一是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
10.三角形三边之比为1:2:$\sqrt{3}$,则三角形中最大角为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 135° |
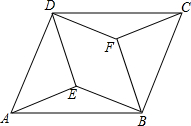 在平行四边形ABCD中,分别以AD,BC为斜边向内作等腰直角△ADE和等腰直角△BCF,连接BE,DF,求证:四边形BEDF是平行四边形.
在平行四边形ABCD中,分别以AD,BC为斜边向内作等腰直角△ADE和等腰直角△BCF,连接BE,DF,求证:四边形BEDF是平行四边形.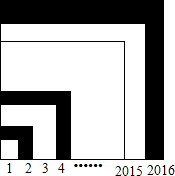 如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1))
如图,边长分别为1,2,3,4,…,2015,2016的正方形叠放在一起,求图中阴影部分的面积.(提示:1+2+3…+n=$\frac{1}{2}$n(n+1)) 已知:如图,△ABC中,∠BAC=100°,在BC边上取点D,使得∠BAD=80°,∠CAD=20°,CE平分∠ACB,联结AD,DE,求∠CED的大小.
已知:如图,△ABC中,∠BAC=100°,在BC边上取点D,使得∠BAD=80°,∠CAD=20°,CE平分∠ACB,联结AD,DE,求∠CED的大小. 如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ=70°.
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ=70°.