题目内容
11.如图1,点O为线段AB上的任意一点(不于A,B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD.
(1)试说明:CB=AD;
(2)如图2,AD与BC相交于点P,∠COD=86°,求∠APB的度数,并说明理由.
分析 (1)证明∠AOD=∠COB,根据“SAS”证明全等;
(2)由∠COD=86°,∠AOC=∠BOD,求出∠AOC,根据△AOD≌△COB,得到∠OAD=∠OCB,由对顶角相等∠CMP=∠AMO,得到∠CPM=∠AOC=47°,根据邻补角求出∠APB.
解答 解:(1)∵∠AOC=∠BOD,
∴∠AOC+∠COD=∠BOD+∠COD,
∴∠AOD=∠COB,
在△AOD和△COB中,
$\left\{\begin{array}{l}{OA=OC}\\{∠AOD=∠COB}\\{OD=OB}\end{array}\right.$
∴△AOD≌△COB.
(2)如图2,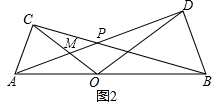
∵∠COD=86°,∠AOC=∠BOD,
∴∠AOC=∠BOD=(180°-86°)÷2=47°,
∵△AOD≌△COB,
∴∠OAD=∠OCB,
∴∠CMP=∠AMO,
∴∠CPM=∠AOC=47°,
∴∠APB=180°-∠CPM=180°-47°=133°.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△AOD≌△COB.

练习册系列答案
相关题目
13.下列说法正确的是( )
①两点之间,线段最短;
②若ab<0,a+b>0,则a,b异号且负数的绝对值大;
③3条直线两两相交最多有3个交点;
④当|a|=-a时,a一定是负数.
①两点之间,线段最短;
②若ab<0,a+b>0,则a,b异号且负数的绝对值大;
③3条直线两两相交最多有3个交点;
④当|a|=-a时,a一定是负数.
| A. | ①②③ | B. | ①③④ | C. | ②④ | D. | ①③ |
6.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 2,3,4 | C. | 1.5,2,2.5 | D. | 6,7,8 |
20.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )
| A. | 125km | B. | 12.5km | C. | 1.25km | D. | 1250km |
1.“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问有多少个小朋友?”若设共有x个小朋友,则列出的方程是( )
| A. | 3x-1=4x+2 | B. | 3x+1=4x-2 | C. | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D. | $\frac{x+1}{3}$=$\frac{x-2}{4}$ |
 在四边形ABCD中,∠BAC+∠BDC=180°,BD=DC,求证:AD平分∠BAC.
在四边形ABCD中,∠BAC+∠BDC=180°,BD=DC,求证:AD平分∠BAC. 如图,已知AB=AC,∠B=∠C,则BD=CD,请说明理由.
如图,已知AB=AC,∠B=∠C,则BD=CD,请说明理由. 如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数.
如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为1.2km.
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为1.2km.