题目内容
2. 在四边形ABCD中,∠BAC+∠BDC=180°,BD=DC,求证:AD平分∠BAC.
在四边形ABCD中,∠BAC+∠BDC=180°,BD=DC,求证:AD平分∠BAC.
分析 过D作DE⊥AB于E,DF⊥AC交AC的延长线于F,根据四边形的内角和得到∠BAC+∠EDF=180°,等量代换即可得到∠BDC=∠EDF,进而得到∠BDE=∠CDF,再证明Rt△BDE≌Rt△CDF,得到DE=DF,所以AD平分∠BAC.
解答 解:如图,过D作DE⊥AB于E,DF⊥AC交AC的延长线于F,
∵DE⊥AB,DF⊥AC,
∴∠AED=90°,∠AFD=90°,
∴∠AED+∠AFD=180°,
∴在四边形AEDF中,∠EAC+∠EDF=360°-(∠AED+∠AFD)=180°,
∵∠BAC+∠BDC=180°,
∴∠BDC=∠EDF,
∴∠BDE+∠EDC=∠EDC+∠CDF,
∴∠BDE=∠CDF,
在Rt△BDE与Rt△CDF中,
$\left\{\begin{array}{l}{∠BED=∠CFD=90°}\\{∠BDE=∠CDF}\\{DB=DC}\end{array}\right.$,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD平分∠BAC.
点评 本题考查了全等三角形的判定和性质,四边形的内角和,角平分线的性质,正确作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
2.下列结论中正确的是( )
| A. | 0既是正数,又是负数 | B. | 0既不是正数,也不是负数 | ||
| C. | 0是最小的正数 | D. | 0是最大的负数 |
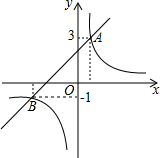 如图,直线y1=x+2与双曲线${y_2}=\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.
如图,直线y1=x+2与双曲线${y_2}=\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1. 如图,已知AD=CB,AE=CF,DE=BF,求证:DE∥BF.
如图,已知AD=CB,AE=CF,DE=BF,求证:DE∥BF.

 如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:AB=CD.
如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:AB=CD.