题目内容
18．阅读下面求y2+4y+8的最小值的解答过程．解：y2+4y+8=y2+4y+4+4=（y+2）2+4
∵（y+2）2≥0
∴（y+2）2+4≥4
∴y2+4y+8的最小值为4．
仿照上面的解答过程，求x2-2x+3的最小值．
分析 多项式配方后，根据完全平方式恒大于等于0，即可求出最小值．
解答 解：x2-2x+3
=x2-2x+1+3-1
=（x-1）2+2≥2，
∵（x-1）2≥0即（x-1）2的最小值为0，
∴x2-2x+3的最小值为2．
点评 此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
数a，b，c在数轴上的位置如图所示，化简式子|a-b|-|b-c|-|a+c|-|b|+2|a|．
9．阅读：在直线上有n个不同的点，则此图中共有多少条线段？通过分析、画图尝试得如下表格：
问题：
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
| 图形 | 直线上点的个数 | 共有线段的条数 | 两者关系 |
 | 2 | 1 | 0+1=$\frac{2×（2-1）}{2}$=1 |
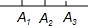 | 3 | 3 | 0+1+2=$\frac{3×（3-1）}{2}$=3 |
 | 4 | 6 | 0+1+2+3=$\frac{4×（4-1）}{2}$=6 |
| … | … | … | … |
 | n |
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点的坐标分别为（-1，0），（3，0）．对于下列结论：①abc＞0，；b2-4ac＞0；③当x1＜x2＜0时，y1＞y2；④当-1＜x＜3时，y＞0．其中正确的有①②③个．
3．把等式ad=bc写成比例式，下列写法错误的是（ ）
| A． | $\frac{a}{b}$=$\frac{c}{d}$ | B． | $\frac{a}{c}$=$\frac{b}{d}$ | C． | $\frac{c}{a}$=$\frac{d}{b}$ | D． | $\frac{a}{d}$=$\frac{b}{c}$ |
10．
反比例函数y=$\frac{k}{x}$（k≠0）的图象在直角坐标系中的位置如图，若点A（-1，y1），B（2，y2），C（3，y3）的在函数y=$\frac{k}{x}$（k≠0）的图象上，则y1，y2，y3的大小关系为（ ）
反比例函数y=$\frac{k}{x}$（k≠0）的图象在直角坐标系中的位置如图，若点A（-1，y1），B（2，y2），C（3，y3）的在函数y=$\frac{k}{x}$（k≠0）的图象上，则y1，y2，y3的大小关系为（ ）| A． | y1＜y2＜y3 | B． | y2＜y1＜y3 | C． | y3＜y2＜y1 | D． | y2＜y3＜y1 |