题目内容
10.在△ABC中,∠A、∠B为锐角,且sinA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$,试判断△ABC的形状?分析 根据特殊角三角函数值,可得答案.
解答 解:由△ABC中,∠A、∠B为锐角,且sinA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$,得∠A=∠B=30°,
△ABC是等腰三角形.
点评 本题考查了特殊角三角函数值,解决此类题目的关键是熟记特殊角的三角函数值.

练习册系列答案
相关题目
19.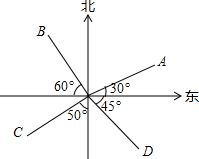 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | OA的方向是北偏东30° | B. | OB的方向是北偏西60° | ||
| C. | OC的方向是南偏东50° | D. | OD的方向是东偏南45° |
20. 如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
 如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
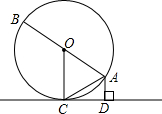 已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.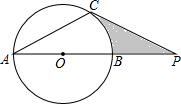 已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP. 如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,