题目内容
2. 如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.
分析 (1)由于点M是AC中点,所以MC=$\frac{1}{2}$AC,由于点N是BC中点,则CN=$\frac{1}{2}$BC,而MN=MC+CN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB,从而可以求出MN的长度;
(2)当C在AB延长线上时,由于点M是AC中点,所以MC=$\frac{1}{2}$AC,由于点N是BC中点,则CN=$\frac{1}{2}$BC,而MN=MC-CN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB,从而可以求出MN的长度.
解答 解:(1)∵点M是AC中点,点N是BC中点,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=MC+CN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=$\frac{1}{2}×6=3$(cm);
(2)当C在AB延长线上时,如图:
∵点M是AC中点,点N是BC中点,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=MC-CN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB=$\frac{1}{2}×6=3$(cm).
点评 本题考查了两点间的距离.不管点C在哪个位置,MC始终等于AC的一半,CN始终等于BC的一半,而MN等于MC加上(或减去)CN等于AB的一半,所以不管C点在哪个位置MN始终等于AB的一半.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.若5x=2,5y=$\frac{1}{2}$,则x,y之间的关系为( )
| A. | x,y互为相反数 | B. | x,y互为倒数 | C. | x=y | D. | 无法判断 |
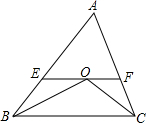 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.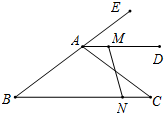 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
 如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.
如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.