题目内容
(1)阅读填空:
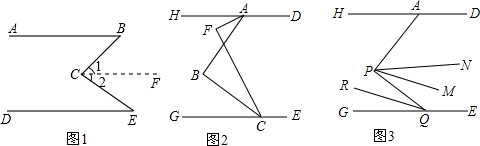
如图1,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
解:∠B+∠E=∠BCE
过点C作CF∥AB,
则∠B=∠1【 】
又∵AB∥DE,AB∥CF,
∴CF∥DE
∴∠E=∠2【 】
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
(2)应用解答:
观察上面图形与结论,解决下面的问题:
如图2,∠DAB+∠B+∠BCE=360°,作∠BCF=∠BCG,CF与∠BAH的平分线交于F,若∠F的余角等于2∠B的补角,求∠BAH的度数.
(3)拓展深化:
如图3,在前面的条件下,若点P是AB上一点,Q是GE上任一点,QR平分∠PQR,PM∥QR,PN平分∠APQ,下列结论:①∠APQ+∠NPM的值不变;②∠NPM的度数不变,可以证明,只有一个是正确的,请你做出正确的选择并求值.

如图1,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
解:∠B+∠E=∠BCE
过点C作CF∥AB,
则∠B=∠1【
又∵AB∥DE,AB∥CF,
∴CF∥DE
∴∠E=∠2【
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
(2)应用解答:
观察上面图形与结论,解决下面的问题:
如图2,∠DAB+∠B+∠BCE=360°,作∠BCF=∠BCG,CF与∠BAH的平分线交于F,若∠F的余角等于2∠B的补角,求∠BAH的度数.
(3)拓展深化:
如图3,在前面的条件下,若点P是AB上一点,Q是GE上任一点,QR平分∠PQR,PM∥QR,PN平分∠APQ,下列结论:①∠APQ+∠NPM的值不变;②∠NPM的度数不变,可以证明,只有一个是正确的,请你做出正确的选择并求值.
考点:平行线的性质
专题:计算题
分析:(1)答案为两直线平行,内错角相等;两直线平行,内错角相等;
(2)首先设∠BAF=x°,∠BCF=y°,过点B作BM∥AD,过点F作FN∥AD,根据平行线的性质,可得∠AFC=(x+2y)°,∠ABC=(2x+y)°,又由∠F的余角等于2∠B的补角,可得方程:90-(x+2y)=180-2(2x+y),继而求得答案.
(3)根据两直线平行,内错角相等可得∠MPQ=∠PQR=
∠PQG,然后根据∠APQ=∠PAH+∠PQG,
列式表示出∠NPM=
∠APQ-
∠PQG=
(∠APQ-∠PQG)=
∠PAH=30°,从而判定②正确.
(2)首先设∠BAF=x°,∠BCF=y°,过点B作BM∥AD,过点F作FN∥AD,根据平行线的性质,可得∠AFC=(x+2y)°,∠ABC=(2x+y)°,又由∠F的余角等于2∠B的补角,可得方程:90-(x+2y)=180-2(2x+y),继而求得答案.
(3)根据两直线平行,内错角相等可得∠MPQ=∠PQR=
| 1 |
| 2 |
列式表示出∠NPM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)故答案为两直线平行,内错角相等;两直线平行,内错角相等;
(2)设∠BAF=x°,∠BCF=y°,
∵∠BCF=∠BCG,CF与∠BAH的平分线交于点F,
∴∠HAF=∠BAF=x°,∠BCG=∠BCF=y°,∠BAH=2x°,∠GCF=2y°,
过点B作BM∥AD,过点F作FN∥AD,
∵AD∥CE,
∴AD∥FN∥BM∥CE,
∴∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,∠ABM=∠BAH=2x°,∠CBM=∠GCB=y°,
∴∠AFC=(x+2y)°,∠ABC=(2x+y)°,
∵∠F的余角等于2∠B的补角,
∴90-(x+2y)=180-2(2x+y),
解得:x=30,
∴∠BAH=60°.
(3)如图,
由(1)可知∠APQ=∠PAH+∠PQG,
∴∠PAH=∠APQ-∠PQG,
∵QR平分∠PQR,PM∥QR,
∴∠MPQ=∠PQR=
∠PQG,
∵PN平分∠APQ,
∴∠NPM=
∠APQ-
∠PQG=
(∠APQ-∠PQG)=
∠PAH,
∵点P是AB上一点,
∴∠PAH=60°,
∴∠NPM=30°;
∴①∠APQ+∠NPM的值随∠DGP的变化而变化;②∠NPM的度数为30°不变.
(2)设∠BAF=x°,∠BCF=y°,
∵∠BCF=∠BCG,CF与∠BAH的平分线交于点F,
∴∠HAF=∠BAF=x°,∠BCG=∠BCF=y°,∠BAH=2x°,∠GCF=2y°,
过点B作BM∥AD,过点F作FN∥AD,
∵AD∥CE,
∴AD∥FN∥BM∥CE,
∴∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,∠ABM=∠BAH=2x°,∠CBM=∠GCB=y°,
∴∠AFC=(x+2y)°,∠ABC=(2x+y)°,
∵∠F的余角等于2∠B的补角,
∴90-(x+2y)=180-2(2x+y),
解得:x=30,
∴∠BAH=60°.
(3)如图,
由(1)可知∠APQ=∠PAH+∠PQG,
∴∠PAH=∠APQ-∠PQG,
∵QR平分∠PQR,PM∥QR,
∴∠MPQ=∠PQR=
| 1 |
| 2 |
∵PN平分∠APQ,
∴∠NPM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵点P是AB上一点,
∴∠PAH=60°,
∴∠NPM=30°;
∴①∠APQ+∠NPM的值随∠DGP的变化而变化;②∠NPM的度数为30°不变.
点评:本题考查了角平分线的定义,平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.此题考查了平行线的性质与判定以及余角、补角的定义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用,理清各角度之间的关系是解题的关键,也是本题的难点.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
下列各组数中,互为倒数的是( )
| A、2和-2 | ||
B、-2和
| ||
C、-2和-
| ||
D、
|
下列说法中正确的是( )
| A、两条直线不相交就平行 |
| B、在同一平面内,两条直线不相交,那么这两条直线平行 |
| C、一条直线的平行线只有一条 |
| D、两条不相交的直线叫做平行线 |
2009个不全相等的有理数之和为0,则这2009个有理数中( )
| A、至少有一个0 |
| B、至少有1005个正数 |
| C、至少有一个是负数 |
| D、至少有2008个负数 |