题目内容
将分别标有数字1、2、3、5的四张质地大小完全相同的卡片背面朝上放在桌面上.
(1)任意抽取一张,求抽到数字是偶数的概率.
(2)任意抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并求出抽取到的两位数大于23的概率.
(1)任意抽取一张,求抽到数字是偶数的概率.
(2)任意抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并求出抽取到的两位数大于23的概率.
考点:列表法与树状图法
专题:计算题
分析:(1)四张卡片中偶数为2,只有一张,求出所求概率即可;
(2)列表得出所有等可能的情况数,找出两位数大于23的情况数,即可求出所求概率.
(2)列表得出所有等可能的情况数,找出两位数大于23的情况数,即可求出所求概率.
解答:解:(1)四张卡片中偶数有一个,
则P(抽到偶数)=
;
(2)列表如下:
所有等可能的情况有12种,其中两位数大于23的情况有7种,
则P(两位数大于23)=
.
则P(抽到偶数)=
| 1 |
| 4 |
(2)列表如下:
| 1 | 2 | 3 | 5 | |
| 1 | --- | 21 | 31 | 51 |
| 2 | 12 | --- | 32 | 52 |
| 3 | 13 | 23 | --- | 53 |
| 5 | 15 | 25 | 35 | --- |
则P(两位数大于23)=
| 7 |
| 12 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a<b,则下列四个不等式中,不正确的是( )
| A、a-2<b-2 |
| B、a-b<0 |
| C、2a>a+b |
| D、-2a>-2b |
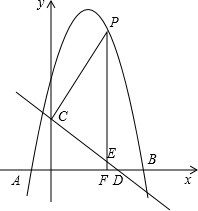 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-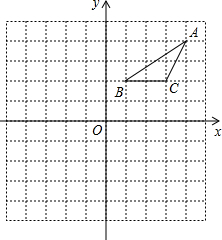 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: 如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走了2015米停下,则这个微型机器人停在
如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走了2015米停下,则这个微型机器人停在