题目内容
 如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m-n-3|+
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m-n-3|+| 2n-6 |
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)根据算术平方根和绝对值的非负性质即可求得m、n的值,即可解题;
(2)连接PB,t秒后,可求得OP=6-t,即可求得S的值;
(3)作出图形,易证∠OBA=∠OPE,只要OP=OB,即可求证△EOP≌△AOB,即可求得t的值,即可解题.
(2)连接PB,t秒后,可求得OP=6-t,即可求得S的值;
(3)作出图形,易证∠OBA=∠OPE,只要OP=OB,即可求证△EOP≌△AOB,即可求得t的值,即可解题.
解答:解:(1)∵|m-n-3|+
=0,
且|m-n-3|≥0,
≥0
∴|m-n-3|=
=0,
∴n=3,m=6,
∴点A(0,6),点B(3,0);
(2)连接PB,
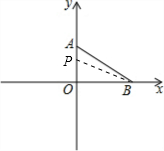
t秒后,AP=t,OP=6-t,
∴S=
OP•OB=
(6-t);
(3)作出图形,
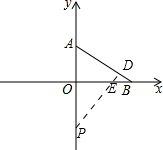
∵∠OAB+∠OBA=90°,∠OAB+∠OPE=90°,
∴∠OBA=∠OPE,
∴只要OP=OB,即可求证△EOP≌△AOB,
∴AP=AO+BO=9,
∴t=9.
| 2n-6 |
且|m-n-3|≥0,
| 2n-6 |
∴|m-n-3|=
| 2n-6 |
∴n=3,m=6,
∴点A(0,6),点B(3,0);
(2)连接PB,

t秒后,AP=t,OP=6-t,
∴S=
| 1 |
| 2 |
| 3 |
| 2 |
(3)作出图形,

∵∠OAB+∠OBA=90°,∠OAB+∠OPE=90°,
∴∠OBA=∠OPE,
∴只要OP=OB,即可求证△EOP≌△AOB,
∴AP=AO+BO=9,
∴t=9.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△EOP≌△AOB是解题的关键.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若2x2-3xy-1-(-x2-7xy+2)=Ax2-Bxy+C,则A,B,C的值分别为( )
| A、3,4,3 |
| B、1,10,1 |
| C、3,4,3 |
| D、3,-4,-3 |
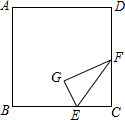 如图,把正方形ABCD的一个角向上折,EF为折痕,点C落在点G处,测得AD=30cm,BE=20cm,∠BEG=60°,求折痕EF的长.
如图,把正方形ABCD的一个角向上折,EF为折痕,点C落在点G处,测得AD=30cm,BE=20cm,∠BEG=60°,求折痕EF的长. 如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于
如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于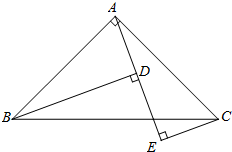 如图,已知△ABC中,∠BAC=90°,AB=AC,B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.求证:
如图,已知△ABC中,∠BAC=90°,AB=AC,B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.求证: