题目内容
12. 如图,已知⊙O的弦AB=3,点C在⊙O上,且∠ACB=60°,则⊙O的直径是2$\sqrt{3}$.
如图,已知⊙O的弦AB=3,点C在⊙O上,且∠ACB=60°,则⊙O的直径是2$\sqrt{3}$.
分析 过A点作直径AD,则∠ABD=90°,∠ADB=∠ACB=60°,在Rt△ABD中,AB=3cm,利用三边的数量关系可求出AD的长.
解答 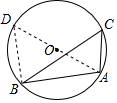 解:过A点作直径AD,连接BD,如图,
解:过A点作直径AD,连接BD,如图,
∠ABD=90°,
又∵∠ADB=∠ACB=60°,
∴∠BAD=30°,
∵AB=3cm,
∴BD=$\frac{AB}{cot30°}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴AD=2BD=2$\sqrt{3}$,即⊙O的直径为 2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了直径所对的圆周角为90度和勾股定理.

练习册系列答案
相关题目

 如图,小明从家到学校有三条路可走,走第②条最近.
如图,小明从家到学校有三条路可走,走第②条最近. 如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.