题目内容
如图,已知抛物线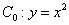 ,顶点记作
,顶点记作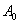 .首先我们将抛物线
.首先我们将抛物线 关于直线
关于直线 对称翻折过去得到抛物线
对称翻折过去得到抛物线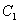 称为第一次操作,再将抛物线
称为第一次操作,再将抛物线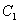 关于直线
关于直线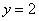 对称翻折过去得到抛物线
对称翻折过去得到抛物线 称为第二次操作,…,将抛物线
称为第二次操作,…,将抛物线 关于直线
关于直线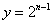 对称翻折过去得到抛物线
对称翻折过去得到抛物线 (顶点记作
(顶点记作 )称为第n此操作(n=1,2,3…),….设抛物线
)称为第n此操作(n=1,2,3…),….设抛物线 与抛物线
与抛物线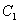 交于两点
交于两点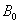 与
与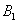 ,顺次连接
,顺次连接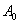 、
、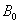 、
、 、
、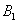 四个点得到四边形
四个点得到四边形 ,抛物线
,抛物线 与抛物线
与抛物线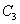 交于两点
交于两点 与
与 ,顺次连接
,顺次连接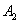 、
、 、
、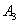 、
、 四个点得到四边形
四个点得到四边形 ,…,抛物线
,…,抛物线 与抛物线
与抛物线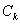 交于两点
交于两点 与
与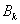 ,顺次连接
,顺次连接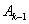 、
、 、
、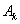 、
、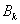 四个点得到四边形
四个点得到四边形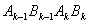 (k=1,3,5…),….
(k=1,3,5…),….
(1)请分别直接写出抛物线 (n=1,2,3,4)的解析式;
(n=1,2,3,4)的解析式;
 (2)一系列四边形
(2)一系列四边形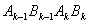 (k=1,3,5…)
(k=1,3,5…)
为哪种特殊的四边形(说明理由)?它们
都相似吗?如果全都相似,请证明之;如
果不全都相似,请举出一对不相似的反例;
(3)试归纳出抛物线 的解析式,无需证明.
的解析式,无需证明.
并利用你归纳出来的 的解析式
的解析式
求四边形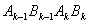 (k=1,3,5…)
(k=1,3,5…)
的面积(用含k的式子表示).
解:(1) ;
; ;
; ;
; ;
;
(2)根据抛物线的对称性以及翻折的原理不难得出四边形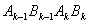 (k=1,3,5…)的两条对角线
(k=1,3,5…)的两条对角线 与
与 互相垂直且平分,故一系列四边形
互相垂直且平分,故一系列四边形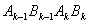 均为菱形;它们并不都相似,反例:四边形
均为菱形;它们并不都相似,反例:四边形 和四边形
和四边形 不相似,
不相似,
理由如下:
不难算出 ,于是四边形
,于是四边形 为正方形.
为正方形.
而 ,
, ,∴
,∴ ,∴四边形
,∴四边形 为菱形,∴它们不相似.
为菱形,∴它们不相似.
(3)抛物线 的解析式为:
的解析式为: ,(或
,(或 .)
.)
由于四边形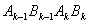 (k=1,3,5…)是抛物线
(k=1,3,5…)是抛物线 关于直线
关于直线 翻折得到抛物线
翻折得到抛物线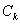 所围成的图形,利用上述结论不难得出:
所围成的图形,利用上述结论不难得出: ,
,
 ,
,
∴ .(或者求解的
.(或者求解的 )
)
∴
 .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列属于平移的是 ( )
|
| A. | 电风扇风叶工作 | B | 电梯的升与降 | C. | 钟摆的摆动 | D. | 方向盘的转动 |
 与
与 的值相等,则
的值相等,则 的值是( )
的值是( )
 的两个实根,且
的两个实根,且 ,
, ;
;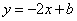 与反比例函数
与反比例函数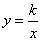 交于点
交于点 的解;
的解;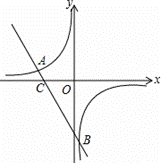
 B.
B. C.
C. D.
D.
 .
.