题目内容
10.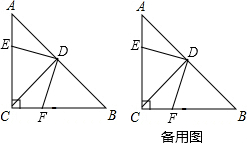 在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.
在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.(1)若AE=CF,试证明DE=DF;
(2)在点E、点F的运动过程中,若DE⊥DF,试判断DE与DF是否一定相等?并加以说明.
(3)在(2)的条件下,若AC=2,四边形ECFD的面积是一个定值吗?若不是,请说明理由,若是,请直接写出它的面积.
分析 (1)根据已知条件,运用SAS判定△DAE≌△DCF,即可得出对应边DE=DF;
(2)根据已知条件,运用ASA判定△DAE≌△DCF,即可得出DE与DF一定相等;
(3)根据△DAE≌△DCF,可得△ADE的面积=△DCF的面积,进而得出四边形ECFD的面积=△DCF的面积+△CDE的面积=△ADE的面积+△CDE的面积=△ACD的面积,再根据△ACD的面积=$\frac{1}{2}$×△ABC的面积=1,即可得出四边形 ECFD的面积是一定值1.
解答 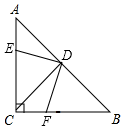 解:(1)∵△ABC中,∠ACB=90°,AC=BC,D是AB的中点,
解:(1)∵△ABC中,∠ACB=90°,AC=BC,D是AB的中点,
∴∠A=∠DCF=45°,CD=$\frac{1}{2}$AB=AD,
在△DAE和△DCF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴△DAE≌△DCF(SAS),
∴DE=DF;
(2)DE与DF一定相等.
证明:∵△ABC中,∠ACB=90°,AC=BC,D是AB的中点,
∴∠A=∠DCF=45°,CD=$\frac{1}{2}$AB=AD,CD⊥AB,
∴∠ADC=∠EDF=90°,
∴∠ADE=∠CDF,
在△DAE和△DCF中,
$\left\{\begin{array}{l}{∠A=∠DCF}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△DAE≌△DCF(ASA),
∴DE=DF;
(3)四边形 ECFD的面积是一定值1.
由(2)可得,△DAE≌△DCF,
∴△ADE的面积=△DCF的面积,
∴四边形ECFD的面积=△DCF的面积+△CDE的面积=△ADE的面积+△CDE的面积=△ACD的面积,
又∵∠ACB=90°,AC=BC=2,
∴△ABC的面积=$\frac{1}{2}$×2×2=2,
又∵D是AB的中点,
∴△ACD的面积=$\frac{1}{2}$×△ABC的面积=1,
即四边形ECFD的面积=1.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质的综合应用,解决问题的关键是掌握:两边及其夹角分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等.

 考前必练系列答案
考前必练系列答案| A. |  三脚猫 | B. |  金丝猫 | C. |  金狮子 | D. |  东北虎 |
 如图,在所标识的角中,互为同旁内角的两个角是( )
如图,在所标识的角中,互为同旁内角的两个角是( )| A. | ∠1和∠3 | B. | ∠2和∠3 | C. | ∠1和∠4 | D. | ∠1和∠2 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
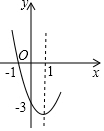 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )| A. | -1<x<4 | B. | x<-1或x>3 | C. | x<-1或x>4 | D. | -1<x<3 |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
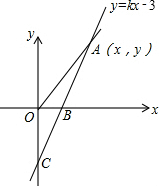 如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB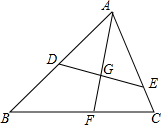 如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.