题目内容
3. 如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.
如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
分析 (1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出一次函数解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
解答 解:(1)∵抛物线y=(x+2)2+m经过点A(-1,0),
∴0=1+m,
∴m=-1,
∴抛物线解析式为y=(x+2)2-1=x2+4x+3,
∴点C坐标(0,3),
∵对称轴x=-2,B、C关于对称轴对称,
∴点B坐标(-4,3),
∵y=kx+b经过点A、B,
∴$\left\{\begin{array}{l}{-4k+b=3}\\{-k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴一次函数解析式为y=-x-1,
(2)由图象可知,写出满足(x+2)2+m≥kx+b的x的取值范围为x≤-4或x≥-1.
点评 本题考查二次函数与不等式、待定系数法等知识,解题的关键是灵活运用待定系数法确定好像解析式,学会利用图象根据条件确定自变量取值范围,属于中考常考题型.

练习册系列答案
相关题目
13. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 该村人均耕地面积y与总人口x成正比例 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 当该村总人口为50人时,人均耕地面积为1公顷 |
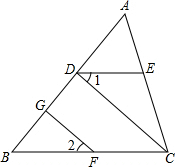 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE 如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(2,0)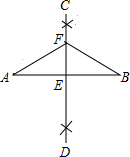 如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.
如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5. 如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为10.
如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为10.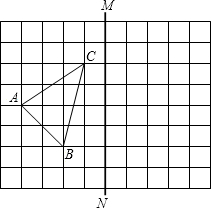 如图,在10×8的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在10×8的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).