题目内容

8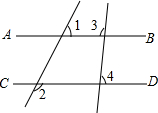．如图，已知直线AB、CD被直线l1，l2所截，若∠1+∠2=180°，∠3=98°，则∠4的度数为82°．

分析 先根据∠1+∠2=180°得出∠5+∠6=180°，故可得出AB∥CD，再由补角的定义得出∠7的度数，根据平行线的性质即可得出结论．

解答 解：∵∠1+∠2=180°，
∴∠5+∠6=180°，
∴AB∥CD．
∵∠3=98°，
∴∠7=180°-98°=82°．
∵AB∥CD，
∴∠4=∠7=82°．
故答案为：82°．

点评 本题考查的是平行线的判定与性质，熟知同旁内角互补，两直线平行是解答此题的关键．

练习册系列答案
相关题目
2．已知抛物线c1：y=ax2+bx+c的顶点为（2，-4），且开口向上，形状和抛物线c2：y=（$\sqrt{m-2}$+1）x2+$\sqrt{2-m}$x+2015m相同，直线y=kx-4交抛物线y=ax2+bx+c于A，B两点．
（1）请你直接写出抛物线c1的解析式；
（2）若△AOB的外心正好在线段AB上，求k的值；
（3）已知点M为直线y=kx-4上的一个定点，N点为为抛彻线c1上的点，Q为线段MN的中点，设点N在执物线c1上运动时，Q的运动轨迹为c3，求c3的解析式．
3．化简：
（1）$\sqrt{72}$；（2）$\sqrt{48}$；（3）$\sqrt{\frac{2}{3}}$；
（4）-2$\sqrt{\frac{9}{2}}$；（5）$\sqrt{{a}^{3}b}$（a≤0）；（6）$\sqrt{{a}^{4}+2{a}^{2}{b}^{2}+{b}^{4}}$．
20．如果|a|=4，|b-1|=3，且a＜b，试求a-b的值．
3．若二次函数y=x2+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解是（　　）
A．x1=0  x2=4B．x1=1  x2=5C．x1=1  x2=-5D．x1=-1  x2=5
13．下列说法正确的是（　　）
A．平方根是它本身的有0，1
B．过一点有且仅有一条直线与已知直线平行
C．$\sqrt{16}$的算术平方根为4
D．垂线段最短
20．两个三角形有以下元素对应相等，则不能确定全等的是（　　）
A．SSAB．SASC．AASD．SSS
17．如图，AB为⊙O的直径，CF切⊙O于点C，BF⊥CF于点F，点D在⊙O上，CD交AB于点E，∠BCE=∠BCF．
（1）求证：弧AC=弧AD；
（2）点G在⊙O上，∠GCD=∠FCD，连接DO并延长交CG于点H，求证：CH=GH；
（3）在（2）的条件下，连接AG，AG=3，CF=2$\sqrt{13}$，求CG的长．
18．现在的时间是9点30分，时钟面上的时针与分针的夹角是（　　）
A．90°B．100°C．105°D．107°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网