题目内容
4．我国汉代数学家赵真为了证明勾股定理，创制了一幅“弦图”，后人称其为“最美弦图”（如图1），图2由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=19，则S2的值是$\frac{19}{3}$．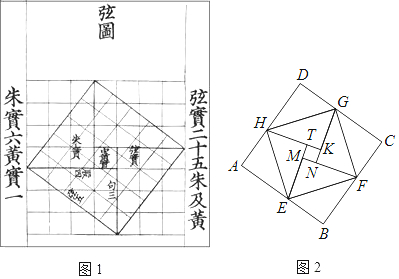
分析 根据图形的特征得出四边形MNKT的面积设为x，将其余八个全等的三角形面积一个设为y，从而用x，y表示出S1，S2，S3，得出答案即可．
解答 解：将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，
∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3=19，
∴得出S1=8y+x，S2=4y+x，S3=x，
∴S1+S2+S3=3x+12y=19，故3x+12y=19，
x+4y=$\frac{19}{3}$，
所以S2=x+4y=$\frac{19}{3}$．
故答案为：$\frac{19}{3}$．
点评 此题主要考查了勾股定理的证明，图形面积关系，根据已知得出用x，y表示出S1，S2，S3，再利用S1+S2+S3=19求出是解决问题的关键．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图，把一个正方形纸片对折两次，然后沿图中虚线剪下一个角，若打开后得到一个正方形纸片，则剪切线与折痕所成的角α的度数等于45°．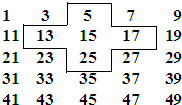
将连续的奇数1，3，5，7，9，…，排成如图所示的数阵．