题目内容
8.若抛物线y=x2+(m-1)x+(m+3)的顶点在坐标轴上,则m的值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由于抛物线的顶点在坐标轴上,故应分在x轴上与y轴上两种情况进行讨论.
解答 解:①当抛物线y=x2+(m-1)x+(m+3)的顶点在x轴上时,
△=(m-1)2-4×(m+3)=0,
整理,得m2-6m-11=0,
解得m=3±2$\sqrt{5}$;
②当抛物线y=x2+(m-1)x+(m+3)的顶点在y轴上时,
m-1=0,
解得m=1.
故选C.
点评 本题考查的是二次函数的性质,抛物线y=ax2+bx+c的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),顶点在坐标轴上时,横坐标为0或者纵坐标为0,解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列事件是必然事件的是( )
| A. | 打开电视机,它正在播放动画片 | |
| B. | 播下一颗种子,种子一定会发芽 | |
| C. | 买100张中奖率为1%的彩票一定会中奖 | |
| D. | 太阳从东方升起 |
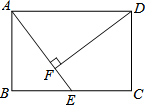 如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.
如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.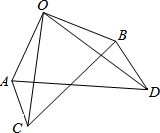 已知:如图,△AOC≌△BOD.求证:△AOD≌△BOC.
已知:如图,△AOC≌△BOD.求证:△AOD≌△BOC. 如图,菱形ABCD周长为8cm,∠BAD=60°,则菱形的面积是2$\sqrt{3}$cm2.
如图,菱形ABCD周长为8cm,∠BAD=60°,则菱形的面积是2$\sqrt{3}$cm2.