题目内容
1.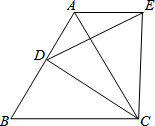 如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.
如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.
分析 先证明∠BCD=∠ACE,再由SAS证明△BCD≌△ACE,得出对应角相等∠DBC=∠EAC=60°,即可得出∠DAE=∠BAC+∠CAE=120°.
解答 解:不发生变化,∠DAE=120°;理由如下:
∵△ABC和△EDC中,
∴BC=AC,∠B=∠ACB=∠BAC=∠DCE=60°,CD=CE,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{BC=AC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴∠DBC=∠EAC=60°,
∴∠DAE=∠BAC+∠CAE=120°.
点评 本题考查了等边三角形的性质以及全等三角形的判定与性质;熟记等边三角形的性质、证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.以下列各组数为边长,能构成直角三角形的是( )
| A. | 3,3,7 | B. | 3,5,8 | C. | 1.5,2,3 | D. | 6,8,10 |
11.0.027的立方根是( )
| A. | 0.3 | B. | ±0.3 | C. | 0.03 | D. | ±0.03 |
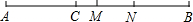 如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点.
如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点. 将长方形纸条折成如图形状,BC为折痕,若∠ABC=55°,那么∠DBA=70°.
将长方形纸条折成如图形状,BC为折痕,若∠ABC=55°,那么∠DBA=70°. 如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°.
如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°.