题目内容

20．观察下列各式：
 1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，1+3+5+7+9+11=36=62，…
你从中发现了什么规律？试用含有字母的式子表示这个规律．

分析 仔细观察题中给出的等式可发现从1开始的连续2个奇数和是22，连续3个奇数和是32，连续4个，5个奇数和分别为42，52…从而推出1开始的连续n个奇数的和：1+3+5+7+…+（2n-1）=n2根据此规律解题即可．

解答 解：∵1+3=4=22，
1+3+5=9=32，
1+3+5+7=16=42，
1+3+5+7+9=25=52，
1+3+5+7+9+11=36=62，
…
∴从1开始的连续n个奇数的和：1+3+5+7+…+（2n-1）=n2．

点评 此题考查数字的变化规律，找出数字之间的运算规律，利用规律，解决问题．

练习册系列答案
相关题目
10．实数a，b，c在数轴上的对应点如图所示，化简a+|a+b|-|b-c|-|b+c-a|=b-a．
11．用代入消元法解下列方程组：
（1）$\left\{\begin{array}{l}{x-3y=2}\\{y=x}\end{array}\right.$；
（2）$\left\{\begin{array}{l}{x+y=5}\\{2x+y=8}\end{array}\right.$；
（3）$\left\{\begin{array}{l}{4x+3y=5}\\{x-2y=4}\end{array}\right.$；
（4）$\left\{\begin{array}{l}{m-\frac{n}{2}=2}\\{2m+3n=12}\end{array}\right.$．
8．已知三个有理数a，b，c的积是正数，它们的和是负数，当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时，求代数式：-3x19-2008x-2013的值．
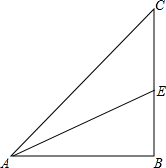15．如图，在Rt△ABC的场地上，∠B=90°，AB=BC，∠CAB的平分线AE交BC于点E．甲、乙两人同时从A处出发，以相同的速度分别沿AC和A→B→E线路前进，甲的目的地为C，乙的目的地为E，请你判断一下，甲、乙两人谁先到达各自的目的地？请说明理由．
5．计算：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{96×97}$=$\frac{96}{97}$．
12．已知有理数a，b，c，其积是负数，其和是正数，当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时，求式子x2014-2015x+2016的值．
9．用计算器计算并填空．
①11-2=9=（　　）2
②1111-22=1089=（　　）2
③111111一222=110889=（　　）2 
④11111111-2222=11108889=（　　）2
（1）你发现了什么规律？
（2）不用计算器，$\underset{\underbrace{111…111}}{2006个}-\underset{\underbrace{222…222}}{1003个}$=（　　）2．
6．下列各组条件中，能判定△ABC≌△DEF的是（　　）
A．AB=DE，BC=EF，∠A=∠DB．∠A=∠D，∠C=∠F，AC=EF
C．AB=DE，BC=EF，AC=DFD．∠B=∠E

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网