题目内容
6．把不等式x-1＞1的解集表示在数轴上，正确的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 先求出不等式的解集，再在数轴上表示出来即可．
解答 解：x-1＞1，
x＞2，
在数轴上表示为：
，
故选B．
点评 本题考查了解一元一次不等式，在数轴上表示不等式的解集的应用，能在数轴上表示不等式的解集是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．满足m2+n2+2m-6n+10=0的是（ ）
| A． | m=1，n=3 | B． | m=1，n=-3 | C． | m=-1，n=3 | D． | m=-1，n=-3 |
17．
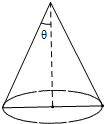已知圆锥的底面半径为5cm，侧面积为60πcm2，设圆锥的母线与高的夹角为θ，则sinθ的值为（ ）
已知圆锥的底面半径为5cm，侧面积为60πcm2，设圆锥的母线与高的夹角为θ，则sinθ的值为（ ）| A． | $\frac{3}{13}$ | B． | $\frac{5}{13}$ | C． | $\frac{5}{12}$ | D． | $\frac{12}{13}$ |
14．某批发店将进价为4元的小商品按5元卖出时，可卖出500件，已知这种商品每件涨价1元，其销售量就减少10件，若要赚得5600元利润，售价应定为（ ）
| A． | 20元 | B． | 39元 | C． | 20元或39元 | D． | 50元 |
1．化简（a2-2+a-2）÷（a2-a-2）的结果为（ ）
| A． | 1 | B． | -1 | C． | $\frac{{a}^{2}-1}{{a}^{2}+1}$ | D． | $\frac{{a}^{2}+1}{{a}^{2}-1}$ |
11．有5名同学参加演讲比赛，以抽签的方式决定每个人的出场顺序，签筒中有5根形状大小相同的纸签，上面分别标有出场的序号1，2，3，4，5．小军首先抽签，他在看不到纸签上的数字的情况下从签筒中随机地抽取一根纸签，下列事件是随机事件的是（ ）
| A． | 抽取一根纸签，抽到的序号是0 | |
| B． | 抽取一根纸签，抽到的序号小于6 | |
| C． | 抽取一根纸签，抽到的序号是1 | |
| D． | 抽取一根纸签，抽到的序号有6种可能的结果 |
如图在3×4的网格中，每个小正方形的边长都是1个单位长度，定义：以网格中小正方形的顶点为顶点的正方形叫作格点正方形，图中包含“△”的格点正方形的个数有（ ）
15．要使分式$\frac{1}{2-x}$有意义，则x的取值范围是（ ）
| A． | x＞2 | B． | x＜2 | C． | x≠-2 | D． | x≠2 |
16．若（am+1bn+2）（a2n-1b2m）=a3b5，则m+n的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | -3 |