题目内容
纽约与北京的时差为-13小时,李伯伯在北京乘坐早晨8:00的航班飞行约20小时到达纽约,则李伯伯到达纽约时间是 时.
考点:有理数的加减混合运算
专题:计算题
分析:根据题意列出算式,计算即可得到结果.
解答:解:根据题意得:8+20-13=15(时),
则李伯伯到达纽约时间是下午15时,
故答案为:15.
则李伯伯到达纽约时间是下午15时,
故答案为:15.
点评:此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知(5,-1)是双曲线y=
(k≠0)上的一点,则下列各点中不在该图象上的是( )
| k |
| x |
A、(
| ||
| B、(5,1) | ||
| C、(-1,5) | ||
D、(10,-
|
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、5
| ||||||||
D、2
|
等腰三角形的一腰上的高与另一腰的夹角是48°,它的一个底角的度数是( )
| A、48° |
| B、21° |
| C、21°或69° |
| D、48°或69° |
将一元一次方程3x2-1=6x化成一般形式后,二次项系数和一次项系数分别为( )
| A、3,-6 |
| B、3,6 |
| C、3,-1 |
| D、3x2,-6x |
下列运算正确的是( )
| A、4x2y-xy2=3x2y |
| B、3(x-1)=3x-1 |
| C、-3a+7a+1=-10a+1 |
| D、-(x-6)=-x+6 |
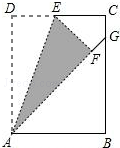 如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为
如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为