题目内容
 已知:(
已知:(| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
(1)用含有n的等式表示上述变化规律:
(2)OA2010=
(2)求S12+S22+S32+…+S20102的值.
考点:勾股定理
专题:规律型
分析:(1)仔细对比题干中给出各个等式,可以得出规律;
(2)根据Sn=
×1•OAn即可求解;
(3)将Sn=
×1•OAn代入代数式,即可求得S12+S22+S32+…+S20102的值,即可解题.
(2)根据Sn=
| 1 |
| 2 |
(3)将Sn=
| 1 |
| 2 |
解答:解:(1)Sn=
;
(2)∵S2010=
×1•OA2010=
,
∴OA2010=
;
(3)S12+S22+S32+…+S20102=(
)2+(
)2+…+(
)2
=
(1+2+3…+2010)
=
×
=
.
故答案为 Sn=
,
.
| ||
| 2 |
(2)∵S2010=
| 1 |
| 2 |
| ||
| 2 |
∴OA2010=
| 2010 |
(3)S12+S22+S32+…+S20102=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
| 2010(1+2010) |
| 2 |
=
| 2021055 |
| 4 |
故答案为 Sn=
| ||
| 2 |
| 2010 |
点评:本题考查了勾股定理的运用,考查了发现规律的能力,考查了等差数列的求和,本题中发现规律是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若抛物线y=ax2+bx+c(a<0)的顶点在第三象限,则一元二次方程ax2+bx+c=0的根的情况是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
 景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿? 如图,O为直线AB边上的一点,∠AOC:∠BOC=1:3,OC为∠AOD的平分线
如图,O为直线AB边上的一点,∠AOC:∠BOC=1:3,OC为∠AOD的平分线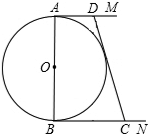 如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC,
如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC, 如图,⊙O的半径为5cm,弦AB=8cm,点P在⊙O上移动,使△PAB的面积为8cm2的点P有且只有
如图,⊙O的半径为5cm,弦AB=8cm,点P在⊙O上移动,使△PAB的面积为8cm2的点P有且只有