题目内容
已知:二次函数y=2x2-4mx+m2.
(1)求证:当m为非零实数时,这个二次函数图象与x轴具有两个不同交点.
(2)若点(3,-4)在这个函数图象上,求解析式.
(1)求证:当m为非零实数时,这个二次函数图象与x轴具有两个不同交点.
(2)若点(3,-4)在这个函数图象上,求解析式.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式
专题:
分析:(1)直接判断b2-4ac的符号,进而得出答案;
(2)将点(3,-4),代入求出二次函数解析式即可.
(2)将点(3,-4),代入求出二次函数解析式即可.
解答:(1)证明:∵b2-4ac=16m2-4×2m2=8m2,m≠0,
∴b2-4ac=8m2>0,
∴这个二次函数的图象与x轴有两个交点;
(2)解:∵这个二次函数的图象经过点(3,-4),
∴-4=2×32-4×3m+m2,
整理得:m2-12m+22=0
解得:m1=6+
,m2=6-
,
故该二次函数的表达式为:y=2x2-4(6+
)x+50+12
或y=2x2-4(6-
)x+50-12
.
∴b2-4ac=8m2>0,
∴这个二次函数的图象与x轴有两个交点;
(2)解:∵这个二次函数的图象经过点(3,-4),
∴-4=2×32-4×3m+m2,
整理得:m2-12m+22=0
解得:m1=6+
| 14 |
| 14 |
故该二次函数的表达式为:y=2x2-4(6+
| 14 |
| 14 |
| 14 |
| 14 |
点评:此题主要考查了抛物线与x轴交点问题,正确将已知点代入求出m的值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
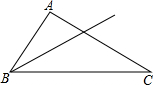 如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )
如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )| A、15° | B、25° |
| C、30° | D、40° |
 指出如图形所示的数轴上的A、B、C、D、E、F各点分别表示什么数?
指出如图形所示的数轴上的A、B、C、D、E、F各点分别表示什么数? 已知:(
已知:(