题目内容
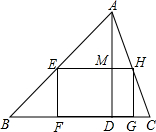 一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.
一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.考点:相似三角形的应用
专题:
分析:根据比例设EH、EF分别为3k、2k,然后根据△AEH和△ABC相似,利用相似三角形对应高的比等于对应边的比列式比例式求出k值,即可得解.
解答:解:∵长方形的长宽比是3:2,
∴设EH、EF分别为3k、2k,
∴EH∥BC,
∴△AEH∽△ABC,
∴
=
,
即
=
,
解得k=
,
∴EH=
米,EF=
米.
∴设EH、EF分别为3k、2k,
∴EH∥BC,
∴△AEH∽△ABC,
∴
| AM |
| AD |
| EH |
| BC |
即
| 1-2k |
| 1 |
| 3k |
| 1.8 |
解得k=
| 3 |
| 11 |
∴EH=
| 9 |
| 11 |
| 6 |
| 11 |
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应高的比等于对应边的比,利用“设k法”表示出边更简便.

练习册系列答案
相关题目
花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,那么0.000037毫克可用科学记数法表示为( )
| A、3.7×10-5毫克 |
| B、3.7×10-6毫克 |
| C、37×10-7毫克 |
| D、3.7×10-8毫克 |
 如图,直线L:y=-
如图,直线L:y=-