题目内容
选择适当的方法解下列方程:
(1)x2+4x+3=0;
(2)
x2-x-2=0.
(1)x2+4x+3=0;
(2)
| 3 |
| 2 |
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:
分析:(1)利用“十字相乘法”对等式的左边进行因式分解;
(2)利用求根公式x=
解方程.
(2)利用求根公式x=
-b±
| ||
| 2a |
解答:解:(1)由原方程,得(x+1)(x+3)=0,
所以 x+1=0或x+3=0,
解得 x1=-1,x2=-3;
(2)∵关于x的一元二次方程
x2-x-2=0的二次项系数a=
,一次项系数b=-1,常数项c=-2,
∴x=
=
=
,
所以 x1=
,x2=
.
所以 x+1=0或x+3=0,
解得 x1=-1,x2=-3;
(2)∵关于x的一元二次方程
| 3 |
| 2 |
| 3 |
| 2 |
∴x=
-b±
| ||
| 2a |
-(-1)±
| ||||
2×
|
1±
| ||
| 3 |
所以 x1=
1+
| ||
| 3 |
1-
| ||
| 3 |
点评:本题考查了解一元二次方程--因式分解法、公式法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
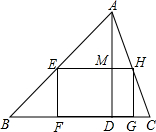 一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.
一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.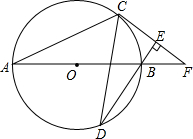 如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
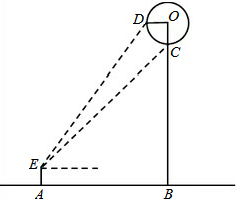 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m) 如图,点A在双曲线
如图,点A在双曲线