题目内容
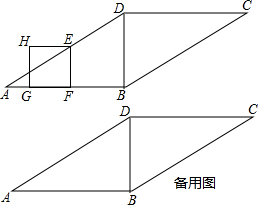
如图,在平行四边形ABCD中,对角线BD与边AB互相垂直,AB=8cm,BD=4cm,点E从A点出发,沿折线AD-DB运动,到点B停止.点E在AD上以
m/s的速度运动,在DB上以1cm/s的速度运动.当点E不与点A重合时,过点E作EF⊥AB于点F,以EF为边作正方形EFGH,使点G落在线段AF上.设E点的运动时间为t(s).
(1)当点H落在AD边上时,求t的值;
(2)在E的运动过程中,正方形EFGH与△ABD重合部分的面积为S(cm2),求S与t的函数关系式;
(3)当点E到过点D时,另一动点P从点C出发,在线段CD上以8cm/s的速度沿C-D-C连续做往返运动,直至点E与点B重合.连接PE,直接写出点P的运动过程中,满足PE∥BC时t的取值.
| 5 |
(1)当点H落在AD边上时,求t的值;
(2)在E的运动过程中,正方形EFGH与△ABD重合部分的面积为S(cm2),求S与t的函数关系式;
(3)当点E到过点D时,另一动点P从点C出发,在线段CD上以8cm/s的速度沿C-D-C连续做往返运动,直至点E与点B重合.连接PE,直接写出点P的运动过程中,满足PE∥BC时t的取值.

考点:相似形综合题
专题:解题思想
分析:(1)根据相似三角形,用t表示相关边长;
(2)重叠部分的面积等于正方形的面积减去三角形的面积;
(3)由两直线平行,得出三角形相似,利用相似比,分类讨论.
(2)重叠部分的面积等于正方形的面积减去三角形的面积;
(3)由两直线平行,得出三角形相似,利用相似比,分类讨论.
解答:解:(1)当点E运动到DB边上时,点H才可能落在AD边上.
在直角△ABD中,AD=8cm,BD=4cm.
由勾股定理,得AD=4
cm.
从点A运动到点D用时间t=4秒,
则DE=t-4,
∵四边形HEFG是正方形,
∴BE=HE=BD-DE=4-(t-4)=8-t.
∵△DEH∽△DBA,
∴
=
,
=
,
解得t=
秒
(2)设HG与AD相交于点I,tan∠A=
=
=
=
,EF=
AF,IG=
AG
①当0<t<4时,∵△AFE∽△ABD,
=
,AE=
t,解得EF=t,AF=2t,GF=t,AG=2t-t=t,IG=
t.HI=
t.S=t2-
×
×t=
t2
②当4<t<
时,设HE与AD相交于点M,tan∠ADF=
=
=2,ME=2DE=2(t-4)=2t-8,GF=EF=4-(t-4)=8-t,AG=AF-GF=8-(8-t)=t,GI=
t.S=(8-t)2-
×
×(16-3t)=
t2-20t+64
③当
<t<8时,正方形EFGH与△ABD重合部分的面积为正方形EFGH,S=(8-t)2=t2-16t+64.
(3)设点E到过点D后,运动的时间为a,∵PE∥BC,∴△DEP∽△DBC,
=
①P在D→C运动时,DP=8-8a,
=
,解得a=
②P在D→C→D运动时,DP=8a-8,
=
,解得a=
③P在D→C→D→C运动时,DP=24-8a,
=
,解得a=
④P在D→C→D→C→D运动时,DP=8a-24,
=
,解得a=4.此时PE与BC重合.
因此满足PE∥BC时t的取值分别为
秒,
秒,
秒.
在直角△ABD中,AD=8cm,BD=4cm.
由勾股定理,得AD=4
| 5 |
从点A运动到点D用时间t=4秒,
则DE=t-4,
∵四边形HEFG是正方形,
∴BE=HE=BD-DE=4-(t-4)=8-t.
∵△DEH∽△DBA,
∴
| DE |
| DB |
| EH |
| AB |
| t-4 |
| 4 |
| 8-t |
| 8 |
解得t=
| 16 |
| 3 |
(2)设HG与AD相交于点I,tan∠A=
| BD |
| AB |
| EF |
| AF |
| IG |
| AG |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①当0<t<4时,∵△AFE∽△ABD,
| AE |
| AD |
| EF |
| BD |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| 3 |
| 4 |
②当4<t<
| 16 |
| 3 |
| AB |
| BD |
| ME |
| DE |
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| 7 |
| 4 |
③当
| 16 |
| 3 |
(3)设点E到过点D后,运动的时间为a,∵PE∥BC,∴△DEP∽△DBC,
| DE |
| DB |
| DP |
| DC |
①P在D→C运动时,DP=8-8a,
| a |
| 4 |
| 8-8a |
| 8 |
| 4 |
| 5 |
②P在D→C→D运动时,DP=8a-8,
| a |
| 4 |
| 8a-8 |
| 8 |
| 4 |
| 3 |
③P在D→C→D→C运动时,DP=24-8a,
| a |
| 4 |
| 24-8a |
| 8 |
| 12 |
| 5 |
④P在D→C→D→C→D运动时,DP=8a-24,
| a |
| 4 |
| 8a-24 |
| 8 |
因此满足PE∥BC时t的取值分别为
| 24 |
| 5 |
| 16 |
| 3 |
| 32 |
| 5 |
点评:考查了相似形综合题,灵活运用相似三角形的性质,难度较大,分类情况较多,考虑要全面.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
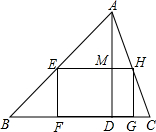 一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.
一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长. 列方程(组)或不等式(组)解应用题:
列方程(组)或不等式(组)解应用题: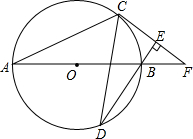 如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.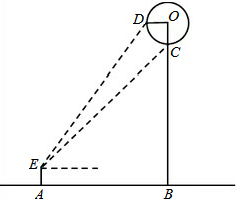 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)