题目内容
 如图,直线L:y=-
如图,直线L:y=-| 1 |
| 2 |
(1)求A、B两点的坐标;
(2)求△COM的面积S与点M的移动时间t之间的函数关系式.
考点:一次函数图象上点的坐标特征
专题:动点型
分析:(1)由直线AB的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=
×OM×OC,求出S与t之间的函数关系式.
(2)由面积公式S=
| 1 |
| 2 |
解答:解:(1)对于直线AB:y=-
x+2,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0),
∴OC=OA=4,
当0≤t≤4时,OM=OA-AM=4-t,
S△OCM=
×4×(4-t)=8-2t;
当t>4时,OM=AM-OA=t-4,
S△OCM=
×4×(t-4)=2t-8.
| 1 |
| 2 |
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0),
∴OC=OA=4,
当0≤t≤4时,OM=OA-AM=4-t,
S△OCM=
| 1 |
| 2 |
当t>4时,OM=AM-OA=t-4,
S△OCM=
| 1 |
| 2 |
点评:此题考查了一次函数图象上点的坐标特征,三角形的面积,进行分类讨论是解题的关键.

练习册系列答案
相关题目
若点(m,n)在函数y=2x+1的图象上,则代数式4m-2n+1的值是( )
| A、1 | B、-1 | C、2 | D、-2 |
 在开展“学雷锋社会实践”活动中,某校为了了解全校200名随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如图.
在开展“学雷锋社会实践”活动中,某校为了了解全校200名随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如图. 在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,
在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,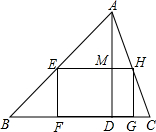 一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长.
一块三角形的余料,底边BC长1.8米,高AD=1米,如图.要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的长EH和宽EF的长. 列方程(组)或不等式(组)解应用题:
列方程(组)或不等式(组)解应用题: