题目内容
(1)解不等式:
-
≤1,并把解集表示在数轴上
(2)解不等式组
,并写出不等式组的整数解.
| 2x-1 |
| 3 |
| 9x+2 |
| 6 |
(2)解不等式组
|
考点:解一元一次不等式,在数轴上表示不等式的解集,解一元一次不等式组,一元一次不等式组的整数解
专题:
分析:(1)首先去分母,然后去括号,移项、合并同类项,系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的整数解即可.
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的整数解即可.
解答:解:去分母,得:2(2x-1)-(9x+2)≤6,
去括号,得:4x-2-9x-2≤6,
移项,得:4x-9x≤6+2+2,
合并同类项,得:-5x≤10,
系数化成1得:x≥-2.
把解集表示在数轴上为:
 ;
;
(2)
,
解①得:x≤4,
解②得:x>2,
则不等式组的解集是:2<x≤4.
则不等式组的整数解是:3,4.
去括号,得:4x-2-9x-2≤6,
移项,得:4x-9x≤6+2+2,
合并同类项,得:-5x≤10,
系数化成1得:x≥-2.
把解集表示在数轴上为:
 ;
;(2)
|
解①得:x≤4,
解②得:x>2,
则不等式组的解集是:2<x≤4.
则不等式组的整数解是:3,4.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知a+b+c=0,则(a+b)(b+c)(c+a)的结果为( )
| A、0 |
| B、-abc |
| C、a2b2c2 |
| D、ab+bc+ca |
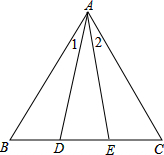 如图,B、D、E、C四点在同一条直线上,且AD=AE,∠1=∠2.求证:∠B=∠C(请不用三角形全等证明).
如图,B、D、E、C四点在同一条直线上,且AD=AE,∠1=∠2.求证:∠B=∠C(请不用三角形全等证明). 在△ABC中,点D在BC上,且∠DAC:∠C:∠B=2:4:3,若AD=BC,求∠B度数.
在△ABC中,点D在BC上,且∠DAC:∠C:∠B=2:4:3,若AD=BC,求∠B度数.