题目内容
已知?ABCD中，AP⊥CD交直线CD于P，当∠PDA=2∠ACD，且AD=5，AP=4时，S?ABCD= ．
考点：平行四边形的性质
专题：
分析：分两种情况：①如图1，当垂足P在CD上时，在PC上截取PE=PD，连结AE；②如图2，当垂足P在CD的延长线上时；分两种情况，根据条件得到CD的长，再根据平行四边形面积公式即可求解．
解答：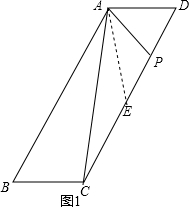
解：①如图1，当垂足P在CD上时，在PC上截取PE=PD，连结AE．
则AE=AD，
∠AED=∠PDA，
∵∠PDA=2∠ACD，∠AED=∠ACD+∠CAE，
∴2∠ACD=∠ACD+∠CAE，
∴∠ACD=∠CAE，
∴CE=AE=AD=5，
∵DE=2PD=2
=6，
∴CD=DE+CE=11，
∴?ABCD的面积=CD•AP=44；
②如图2，当垂足P在CD的延长线上时，
∵∠PDA=2∠ACD，∠PDA=∠ACD+∠CAD，
∴2∠ACD=∠ACD+∠CAD，
∴∠ACD=∠CAD，
∴CD=AD=5，
∴?ABCD的面积=CD•AP=20．
故?ABCD的面积是44或20．
故答案为：44或20．
解：①如图1，当垂足P在CD上时，在PC上截取PE=PD，连结AE．则AE=AD，
∠AED=∠PDA，
∵∠PDA=2∠ACD，∠AED=∠ACD+∠CAE，
∴2∠ACD=∠ACD+∠CAE，
∴∠ACD=∠CAE，
∴CE=AE=AD=5，
∵DE=2PD=2
| AD2-AP2 |
∴CD=DE+CE=11，
∴?ABCD的面积=CD•AP=44；②如图2，当垂足P在CD的延长线上时，
∵∠PDA=2∠ACD，∠PDA=∠ACD+∠CAD，
∴2∠ACD=∠ACD+∠CAD，
∴∠ACD=∠CAD，
∴CD=AD=5，
∴?ABCD的面积=CD•AP=20．
故?ABCD的面积是44或20．
故答案为：44或20．
点评：考查了平行四边形的性质和勾股定理，解题关键是得到CD的长，注意分类思想的应用．
练习册系列答案
应用题作业本系列答案
相关题目
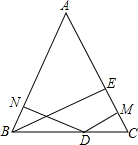如图所示，∠B=∠C，BE⊥AC，DM⊥AC，DN⊥AB，求证：DM+DN=BE．