题目内容
2．已知方程组$\left\{\begin{array}{l}y-2x+3=0\\ 2y+3x-6=0\end{array}\right.$的解为$\left\{\begin{array}{l}x=\frac{4}{3}\\ y=1\end{array}\right.$，则一次函数y=2x-3与y=-$\frac{3}{2}$x+3的交点P的坐标是（$\frac{4}{3}$，1）．分析 利用函数图象交点坐标为两函数解析式组成的方程组的解进行回答．
解答 解：∵方程组$\left\{\begin{array}{l}y-2x+3=0\\ 2y+3x-6=0\end{array}\right.$的解为$\left\{\begin{array}{l}x=\frac{4}{3}\\ y=1\end{array}\right.$，
∴一次函数y=2x-3与y=-$\frac{3}{2}$x+3的交点P的坐标为（$\frac{4}{3}$，1）．
故答案为（$\frac{4}{3}$，1）．
点评 本题考查了一次函数与二元一次方程（组）：函数图象交点坐标为两函数解析式组成的方程组的解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系中，一次函数的图象与坐标轴围成的三角形，叫做此一次函数的坐标三角形．例如，图中的一次函数的图象与x，y轴分别交于点A，B，则△OAB为此函数的坐标三角形．
11．下列各式从左到右的变形，正确的是（ ）
| A． | $\frac{y}{x}$=$\frac{{y}^{2}}{{x}^{2}}$ | B． | $\frac{y}{x}$=$\frac{yz}{xz}$（z≠0） | C． | $\frac{y}{x}$=$\frac{y-m}{x-m}$ | D． | $\frac{y}{x}$=$\frac{y+n}{x+n}$（n≠0） |
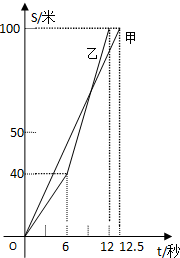甲、乙两同学在一次百米赛跑中，路程S（米）与时间t（秒）之间的关系如图所示．根据图象回答下列问题：