题目内容
17.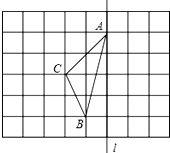 如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)求△ABC的面积为4;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为$\sqrt{13}$.
分析 (1)利用轴对称图形的性质得出各对应点进而求出即可;
(2)利用△ABC所在矩形的面积减去周围三角形面积进而求出即可;
(3)利用轴对称图形的性质得出P点位置,进而利用勾股定理求出即可.
解答  解:(1)如图所示:△AB′C′即为所求;
解:(1)如图所示:△AB′C′即为所求;
(2)△ABC的面积为:2×4-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×1×2=4;
故答案为:4;
(3)如图所示:P点即为所求,PB+PC的长为BC′的长,则BC′=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 此题主要考查了轴对称变换以及勾股定理等知识,得出各对应点位置是解题关键.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
6. 如图,点A、B、C是⊙O上,∠AOB=80°,则∠ACB的度数为( )
如图,点A、B、C是⊙O上,∠AOB=80°,则∠ACB的度数为( )
 如图,点A、B、C是⊙O上,∠AOB=80°,则∠ACB的度数为( )
如图,点A、B、C是⊙O上,∠AOB=80°,则∠ACB的度数为( )| A. | 40° | B. | 80° | C. | 120° | D. | 160° |
 仔细想一想,完成下面的推理过程.
仔细想一想,完成下面的推理过程.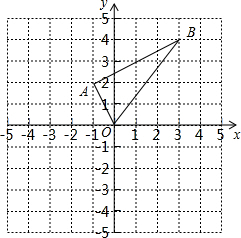 如图在平面直角坐标系中,已知点A(-1,2),B(3,4).
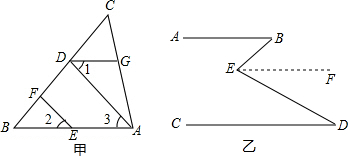
如图在平面直角坐标系中,已知点A(-1,2),B(3,4).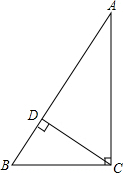 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.