题目内容
 如图,∠B=90°,ED垂直平分AC,AE平分∠BAC.若AB=1,则AC=
如图,∠B=90°,ED垂直平分AC,AE平分∠BAC.若AB=1,则AC=考点:线段垂直平分线的性质,全等三角形的判定与性质,角平分线的性质
专题:
分析:先根据线段垂直平分线的性质得出∠C=∠CAE,再由AE平分∠BAC得出∠C=∠CAE=∠BAE,由直角三角形的性质求出∠C的度数,进而可得出结论.
解答:解:∵ED垂直平分AC,
∴∠C=∠CAE,
∵AE平分∠BAC,
∴∠C=∠CAE=∠BAE,
∵∠B=90°,
∴∠BAC+∠C=90°,即3∠C=90°,解得∠C=30°.
∵AB=1,
∴AC=2AB=2.
故答案为:2.
∴∠C=∠CAE,
∵AE平分∠BAC,
∴∠C=∠CAE=∠BAE,
∵∠B=90°,
∴∠BAC+∠C=90°,即3∠C=90°,解得∠C=30°.
∵AB=1,
∴AC=2AB=2.
故答案为:2.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知平面上四点A,B,C,D,利用尺规按下列要求作图:
如图,已知平面上四点A,B,C,D,利用尺规按下列要求作图: 已知:如图,OM平分∠AOB,ON平分∠BOC.
已知:如图,OM平分∠AOB,ON平分∠BOC. 如图,在△ABC中,∠ACB=90°,cosB=
如图,在△ABC中,∠ACB=90°,cosB= 如图,已知矩形ABCD中,AC=25,AB=7,对角线AC上按如图方式串有5个大小不一样的矩形,则这5个矩形的周长之和
如图,已知矩形ABCD中,AC=25,AB=7,对角线AC上按如图方式串有5个大小不一样的矩形,则这5个矩形的周长之和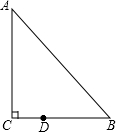 如图,Rt△ABC中,已知∠C=90°,∠B=48°,点D在边BC上,BD=2CD,把Rt△ABC绕点D逆时针旋转m(0°<m<180°)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
如图,Rt△ABC中,已知∠C=90°,∠B=48°,点D在边BC上,BD=2CD,把Rt△ABC绕点D逆时针旋转m(0°<m<180°)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=