题目内容
8.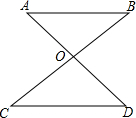 如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.
如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.①∠A=∠D;②∠B=∠C;③AB=CD;④BO=OC;⑤AB∥CD.
分析 由ASA得出①②⑤正确,由SAS得出④正确,即可得出结果.
解答 解:∵OA=OD,而∠AOB=∠DOC,
∴当∠A=∠D,或∠B=∠C时,
可利用“ASA”证明△ABO≌△DCO.
∴①②正确;
∵OA=OD,而∠AOB=∠DOC,
∴当BO=OC,可利用“SAS”证明△ABO≌△DCO.
∴③正确;
当AB∥CD时,∠A=∠D,
可利用“ASA”证明△ABO≌△DCO;
当AB=CD时,由“SSA”不能证明△ABO≌△DCO;
∴能证明△ABO≌△DCO,这样的条件有①②④⑤;
故答案为:①②④⑤.
点评 本题考查了全等三角形的判定方法;熟记全等三角形的判定方法是解决问题的关键:.

练习册系列答案
相关题目
16.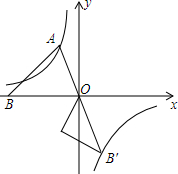 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
1.已知一次函数y=kx+b的图象经过第一、二、四象限,则函数y=$\frac{kb}{x}$的图象在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第三、四象限 | D. | 第一、二象限 |
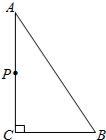 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).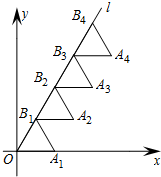 如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).
如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).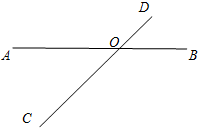 如图,直线AB,CD相交于点O,∠AOD=3∠BOD+20°,则∠BOD=40°.
如图,直线AB,CD相交于点O,∠AOD=3∠BOD+20°,则∠BOD=40°. 如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求BC的长.
如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求BC的长.