题目内容
3.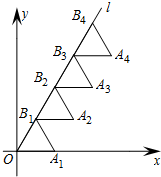 如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).
如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).
分析 根据题意得出直线B2B1的解析式为:y=$\sqrt{3}$x,进而得出B1,B2,B3坐标,进而得出坐标变化规律,进而得出答案.
解答 解:过B1向x轴作垂线B1C,垂足为C,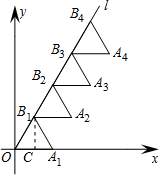
由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,
∴CB1=OB1cos30°=$\frac{\sqrt{3}}{2}$,
∴B1的横坐标为:$\frac{1}{2}$,则B1的纵坐标为:$\frac{\sqrt{3}}{2}$,
∴点B1,B2,B3,…都在直线y=$\sqrt{3}$x上,
∴B1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
同理可得出:A1的横坐标为:1,
∴y=$\sqrt{3}$,
∴A1(2,$\sqrt{3}$),
…
An(1+$\frac{n+1}{2}$,$\frac{(n+1)\sqrt{3}}{2}$).
∴A2015(1008,1007$\sqrt{3}$).
故答案为(1008,1007$\sqrt{3}$).
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
14.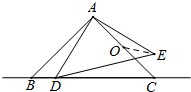 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
 如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.
如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.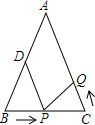 如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.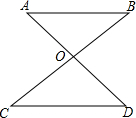 如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.
如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.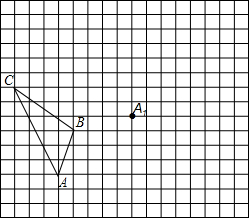 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.画出△ABC关于点A1的中心对称图形.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.画出△ABC关于点A1的中心对称图形.